Оглавление:

Прежде чем изучать готовые решения задач, нужно знать теорию, поэтому для вас я подготовила очень краткую теорию по предмету «линейная алгебра», после которого, чуть ниже размещены подробные решения задач.
Эта страница подготовлена для школьников и студентов любых специальностей и охватывает полный курс предмета «линейная алгебра».
| Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу! |
Линейная алгебра
Линейная алгебра — это раздел математики, касающийся линейных уравнений. Линейная алгебра занимает центральное место почти во всех областях математики. Например, линейная алгебра является фундаментальной в современных представлениях геометрии, в том числе для определения основных объектов, таких как линии, плоскости и вращения.
Кроме того, функциональный анализ, раздел математического анализа, можно рассматривать как в основном применение линейной алгебры к пространствам функций.
Линейная алгебра также используется в большинстве наук и областей техники , поскольку она позволяет моделировать многие природные явления и эффективно проводить вычисления с такими моделями. Для нелинейных систем, которые не могут быть смоделированы с линейной алгеброй, он часто используются для борьбы с аппроксимациями первого порядка, используя тот факт, что дифференциал из многомерной функции в точке является линейным отображением , что лучше аппроксимирует функцию вблизи этой точки.
Матрицы
Прямоугольная таблица из чисел вида
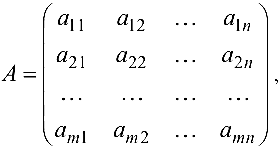
состоящая из 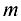 строк и
строк и 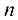 столбцов, называется матрицей размеров
столбцов, называется матрицей размеров
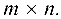
Матрица 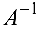 называется обратной к квадратной матрице
называется обратной к квадратной матрице 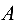 , если
, если 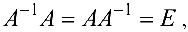 где
где 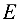 — единичная матрица. Для невырожденной матрицы
— единичная матрица. Для невырожденной матрицы 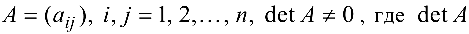 — определитель матрицы
— определитель матрицы 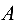 , существует единственная обратная матрица
, существует единственная обратная матрица
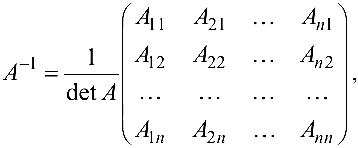
где 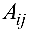 — алгебраические дополнения элементов
— алгебраические дополнения элементов 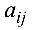 матрицы
матрицы 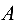 . Если матрица
. Если матрица 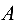 — вырожденная
— вырожденная 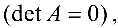 то обратной к пей не существует.
то обратной к пей не существует.
Задача №4.1.
Найти матрицу 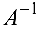 , обратную к матрице
, обратную к матрице
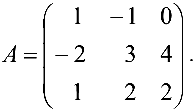
Так как 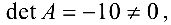 то
то 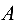 — невырожденная и
— невырожденная и 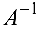 существует. Найдем алгебраические дополнения элементов матрицы
существует. Найдем алгебраические дополнения элементов матрицы 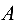 :
:
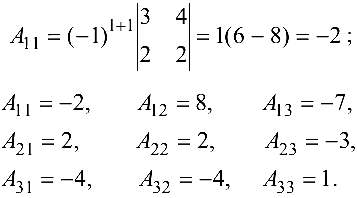
Следовательно,
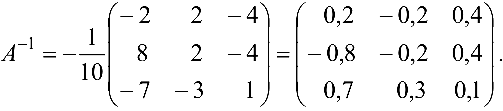
Возможно эта страница вам будет полезна:
| Предмет линейная алгебра |
Системы линейных уравнений. Матричный метод. Правило Крамера. Метод Гаусса
Пусть задана система 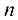 линейных уравнений с
линейных уравнений с 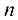 неизвестными вида.
неизвестными вида.
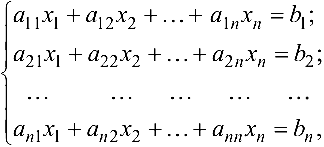
или, в матричной форме
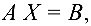
где
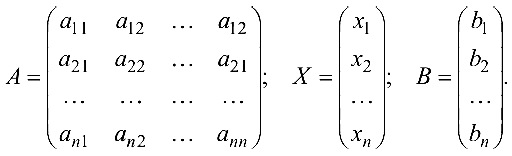
Рассмотрим некоторые методы решения системы (4.1).
Формулы Крамера. Если система (4.1) невырождена, то она имеет единственное решение, определяемое формулами Крамера:
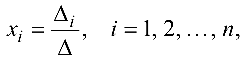
где 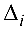 — определитель, получаемый из определителя
— определитель, получаемый из определителя  заменой его
заменой его 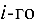 столбца на столбец В свободных членов.
столбца на столбец В свободных членов.
Матричный метод
Решение невырожденной системы (4.1) можно найти по формуле
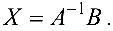
Метод последовательного исключения неизвестных (метод Гаусса).
С помощью элементарных преобразований над строками система 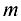 линейных уравнений с
линейных уравнений с 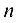 неизвестными может быть приведена к виду
неизвестными может быть приведена к виду
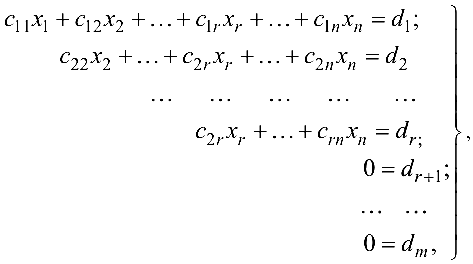
где 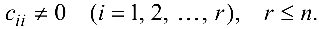
Система (4.2) эквивалентна исходной системе. Если хотя бы одно из чисел 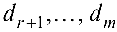 отлично от нуля, то система (4.2), а следовательно, и исходная система несовместны. Если же
отлично от нуля, то система (4.2), а следовательно, и исходная система несовместны. Если же 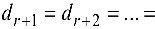
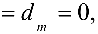 то система совместна и из уравнений (4.2) выражают последовательно неизвестные
то система совместна и из уравнений (4.2) выражают последовательно неизвестные 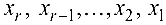 через
через 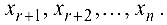
Задача №4.2.
Методом Гаусса решить систему
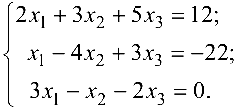
Решение:
Расширенная матрица системы имеет вид
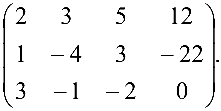
Производя элементарные преобразования над строками расширенной матрицы, получаем
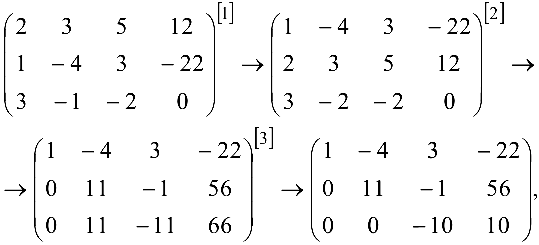
где цифрами [1] , [2] , [3] обозначены следующие операции:
[1] — первую и вторую строки поменяли местами; [2] — ко второй строке прибавили первую, умноженную на (-2): к третьей прибавили первую, умноженную на (-3); [3] — к третьей строке прибавили вторую, умноженную на (-1).
Этой матрице соответствует система
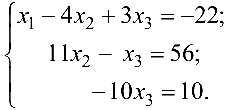
Отсюда последовательно находим
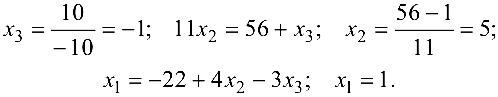
Ответ: 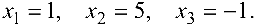
Задача №4.3.
Решить систему уравнений
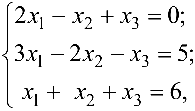
используя формулы Крамера.
Решение:
Так как определитель данной системы
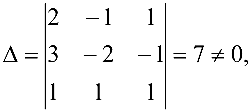
то матрица 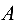 невырождена и система имеет единственное решение. Находим определители
невырождена и система имеет единственное решение. Находим определители 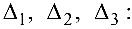
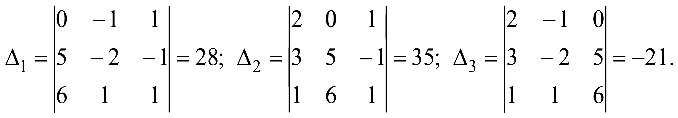
По формулам Крамера находим решение системы:
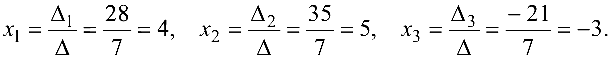
Возможно эта страница вам будет полезна:
| Помощь с линейной алгеброй |
Скалярное произведение векторов в R3
Скалярным произведением векторов 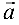 и
и 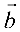 называется число, обозначаемое
называется число, обозначаемое 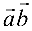 или
или 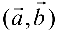 и равное
и равное 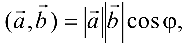 где
где 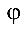 — угол между
— угол между 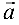 и
и 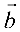 .
.
Свойства скалярного произведения:
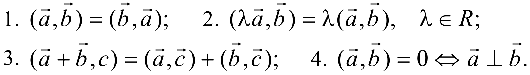
Свойство 4 выражает условие ортогональности векторов.
Если векторы 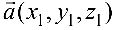 и
и 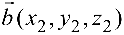 представлены своими координатами в ортонормированном базисе
представлены своими координатами в ортонормированном базисе 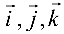 , то скалярное произведение равно
, то скалярное произведение равно 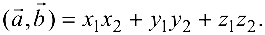
Из этой формулы и определения скалярного произведения следует:
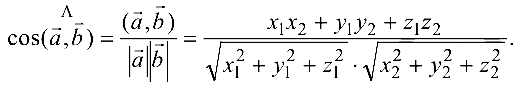
Учитывая, что 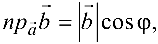 где
где 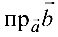 — проекция вектора
— проекция вектора 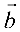 па вектор
па вектор 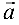 , а
, а 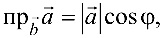 скалярное произведение векторов
скалярное произведение векторов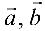 можно записать в виде
можно записать в виде
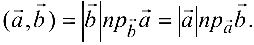
Задача №4.4.
Даны векторы 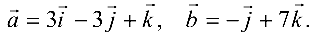
Найти 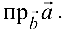
Решение:
Поскольку 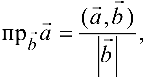
а векторы 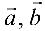 заданы координатами в ортонормированном базисе, то
заданы координатами в ортонормированном базисе, то
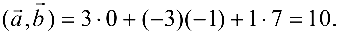
Поэтому
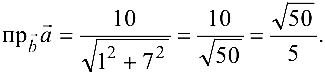
Механический смысл скалярного произведения: работал 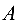 , производимая силой
, производимая силой 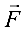 , точка приложения которой перемещается из точки
, точка приложения которой перемещается из точки 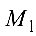 в точку
в точку 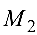 , вычисляется по формуле
, вычисляется по формуле 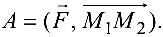
Возможно эта страница вам будет полезна:
| Заказать контрольную работу по линейной алгебре |
Векторное произведение векторов
Упорядоченная тройка некомпланарных векторов 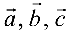 называется правой, если при наблюдении из конца третьего вектора кратчайший поворот от первого ко второму виден против часовой стрелки; в противном случае тройка называется левой (рис. 4.1).
называется правой, если при наблюдении из конца третьего вектора кратчайший поворот от первого ко второму виден против часовой стрелки; в противном случае тройка называется левой (рис. 4.1).
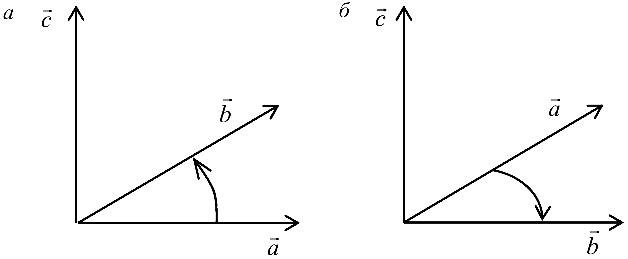
Рис. 4.1: а — тройка 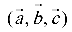 правая; б — тройка
правая; б — тройка 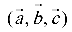 левая
левая
Векторным произведением вектора 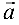 на вектор
на вектор 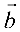 называется вектор с, удовлетворяющий условиям:
называется вектор с, удовлетворяющий условиям:
1) 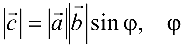 — угол между векторами
— угол между векторами 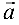 и
и 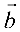 ;
;
2) 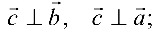
3) Упорядоченная тройка 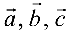 — правая.
— правая.
Обозначение: 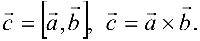
Свойства векторного произведения
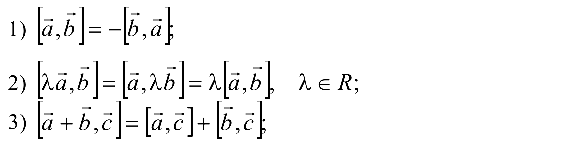
4) 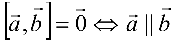 — условие коллинеарности векторов.
— условие коллинеарности векторов.
Если векторы 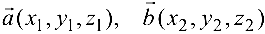 заданы своими координатами в ортонормированном базисе
заданы своими координатами в ортонормированном базисе 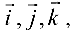 то
то
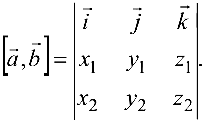
Площадь параллелограмма, построенного на векторах 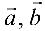 , можно определить по формуле
, можно определить по формуле
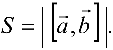
Задача №4.5.
Найти площадь и длину высоты 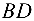 треугольника с вершинами в точках
треугольника с вершинами в точках 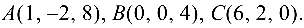
Решение:
Поскольку площадь 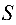 треугольника
треугольника 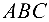 равна
равна
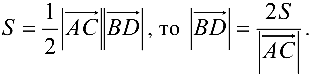
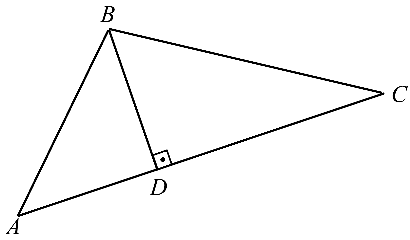
- Находим координаты векторов
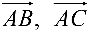 и длину
и длину 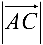 вектора
вектора 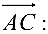
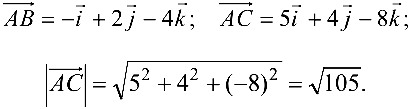
2. Находим 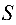 :
:
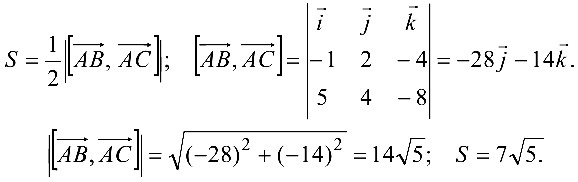
3. 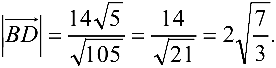
Механический смысл векторного произведения. Пусть точка 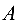 твердого тела закреплена, а в его точке
твердого тела закреплена, а в его точке 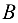 приложена сила
приложена сила 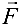 .
.
Тогда возникает вращательный момент 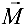 (момент силы). По определению момент силы относительно точки
(момент силы). По определению момент силы относительно точки 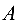 находится по формуле
находится по формуле 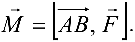
Возможно эта страница вам будет полезна:
| Заказать работу по линейной алгебре |
Смешанное произведение векторов
Смешанным произведением трех векторов 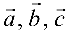 называется число, получаемое следующим образом: векторное произведение
называется число, получаемое следующим образом: векторное произведение 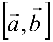 умножается скалярно на вектор
умножается скалярно на вектор 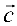 . Смешанное произведение векторов
. Смешанное произведение векторов 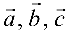 обозначается
обозначается 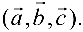 Таким образом,
Таким образом, 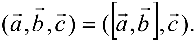 Если векторы
Если векторы 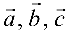 заданы своими координатами в ортонормированном базисе, то
заданы своими координатами в ортонормированном базисе, то
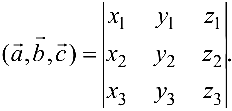
Объем параллелепипеда 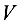 , построенного на векторах
, построенного на векторах 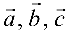 , можно вычислить по формуле
, можно вычислить по формуле 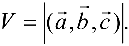 Для того чтобы три вектора
Для того чтобы три вектора 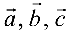 были компланарны, необходимо и достаточно, чтобы
были компланарны, необходимо и достаточно, чтобы 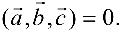
Задача №4.6.
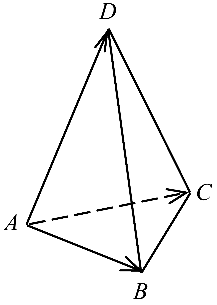
Вычислить объем треугольной пирамиды с вершинами 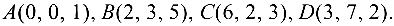
Решение:
Рассмотрим три вектора
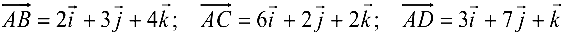
(рис. 4.3).
Можно показать, что объем пирамиды 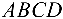 равен шестой части объема параллелепипеда, построенного на векторах
равен шестой части объема параллелепипеда, построенного на векторах 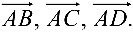
Тогда 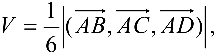 а так
а так
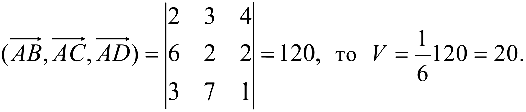
Возможно эта страница вам будет полезна:
| Готовые контрольные работы по линейной алгебре |
Прямая на плоскости
1. Прямая на плоскости
В декартовой прямоугольной системе координат 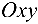 прямая на плоскости может быть задана уравнениями:
прямая на плоскости может быть задана уравнениями:
- общее уравнение прямой
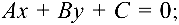 (4.3)
(4.3)
- уравнение прямой, проходящей через точку
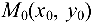 перпендикулярно нормальному вектору
перпендикулярно нормальному вектору 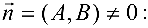
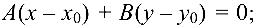
- уравнение прямой, проходящей через точку
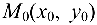 параллельно направляющему вектору
параллельно направляющему вектору 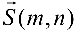 (каноническое уравнение
(каноническое уравнение
прямой):
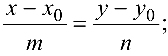
- параметрические уравнения прямой
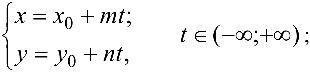
- уравнение прямой в отрезках
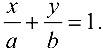
Здесь 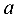 и
и 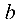 — величины отрезков, отсекаемых на осях координат
— величины отрезков, отсекаемых на осях координат 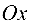 и
и 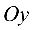 (т.е. длины, взятые с соответствующими знаками);
(т.е. длины, взятые с соответствующими знаками);
- уравнение прямой, проходящей через две данные точки
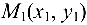 и
и 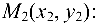
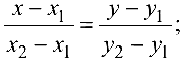
- уравнение прямой с угловым коэффициентом
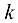 , проходящей через точку
, проходящей через точку 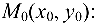
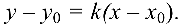
Расстояние 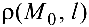 от точки
от точки 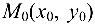 до прямой
до прямой 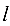 , заданной уравнением (4.3), определяется по формуле
, заданной уравнением (4.3), определяется по формуле
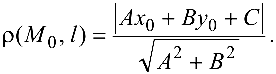
Две прямые, заданные уравнениями 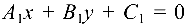 и
и 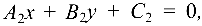 параллельны, если
параллельны, если
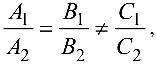
и перпендикулярны, если 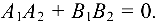
Задача №4.7.
Составить уравнение прямой на плоскости, проходящей через точку 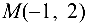 перпендикулярно вектору, проходящему через точки
перпендикулярно вектору, проходящему через точки 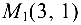 и
и 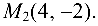 Найти расстояние от точки
Найти расстояние от точки 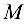 до прямой, проходящей через точки
до прямой, проходящей через точки 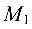 и
и 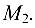
Решение:
Уравнение прямой запишем в виде:
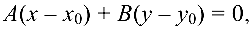
где 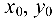 — координаты точки
— координаты точки 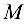 , а
, а 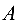 и
и 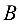 — координаты нормального вектора.
— координаты нормального вектора.
Так как 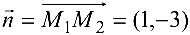 то уравнение имеет вид
то уравнение имеет вид 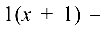
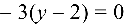 или
или 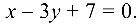
Для нахождения расстояния от точки 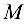 до прямой
до прямой 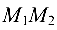 запишем уравнение этой прямой в виде
запишем уравнение этой прямой в виде
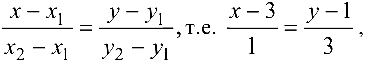
или 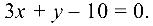
Подставляя в формулу (4.4) координаты 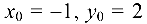 точки
точки 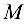 ,
,
получаем
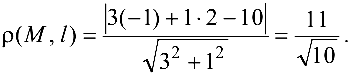
2. Плоскость
Плоскость в прямоугольной системе координат может быть задана уравнениями:
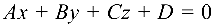 — общее уравнение плоскости. (4.5)
— общее уравнение плоскости. (4.5)
Если в уравнении (4.5) отсутствует свободный член 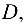 то плоскость проходит через начало координат.
то плоскость проходит через начало координат.
Если в уравнении (4.5) отсутствует одна из переменных, то плоскость параллельна той оси, название которой не входит в это уравнение.
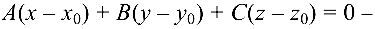
уравнение плоскости, проходящей через точку 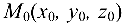 перпендикулярно нормальному вектору
перпендикулярно нормальному вектору 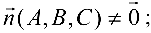
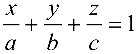 — уравнение плоскости в отрезках,
— уравнение плоскости в отрезках,
где 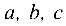 — величина отрезков, отсекаемых плоскостью па координатных осях;
— величина отрезков, отсекаемых плоскостью па координатных осях;
- уравнение плоскости, проходящей через три данные точки
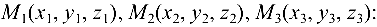
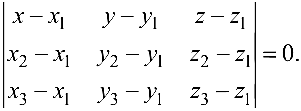
Величина угла 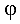 между двумя плоскостями
между двумя плоскостями 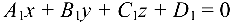 и
и 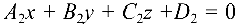 вычисляется по формуле
вычисляется по формуле
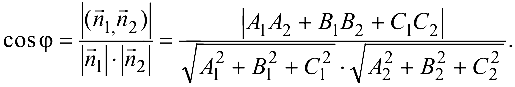
Условие перпендикулярности данных плоскостей запишется в виде
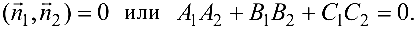
Условие параллельности рассматриваемых плоскостей имеет вид
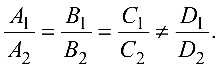
Расстояние 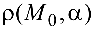 от точки
от точки 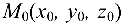 до плоскости
до плоскости 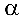 , заданной уравнением (4.5), вычисляется по формуле
, заданной уравнением (4.5), вычисляется по формуле
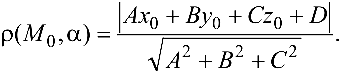
Задача №4.8.
Составить уравнение плоскости, проходящей через точки 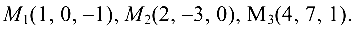
Решение:
Воспользуемся формулой (4.6):
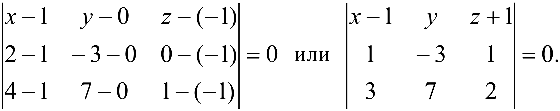
Раскрыв определитель, получаем искомое уравнение плоскости:
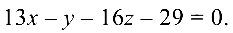
Линии второго порядка
Линией второго порядка называется множество точек плоскости, координаты 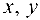 которых в прямоугольной системе координат удовлетворяют уравнению второй степени
которых в прямоугольной системе координат удовлетворяют уравнению второй степени
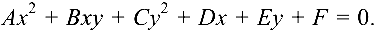
Уравнение (4.7) называется общим уравнением линии второго порядка (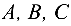 не равны нулю одновременно).
не равны нулю одновременно).
При помощи преобразования прямоугольной системы координат (параллельного переноса и поворота) всегда можно найти такую новую прямоугольную систему координат, в которой уравнение (4.7) имеет один из следующих трех видов (каноническое уравнение):
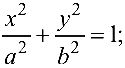
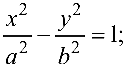
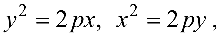
где 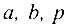 — положительные числа. Уравнение (4.7) может определять так называемую вырожденную кривую (пустое множество, точку, прямую, пару прямых).
— положительные числа. Уравнение (4.7) может определять так называемую вырожденную кривую (пустое множество, точку, прямую, пару прямых).
При этом линия, приводимая к виду (4.8), (4.9), (4.10), называется соответственно эллипсом, гиперболой или параболой.
Эллипс с каноническим уравнением 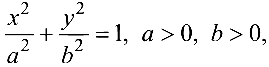
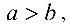
имеет форму, изображенную на рис. 4.4.
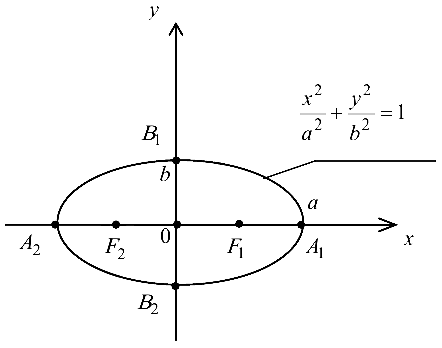
Точки 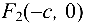 и
и 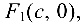 где
где 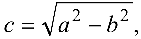 называются фокусами эллипса.
называются фокусами эллипса.
Числа 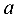 и
и 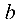 называются полуосями эллипса.
называются полуосями эллипса.
Гипербола с каноническим уравнением 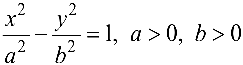
имеет форму, изображенную на рис. 4.5.
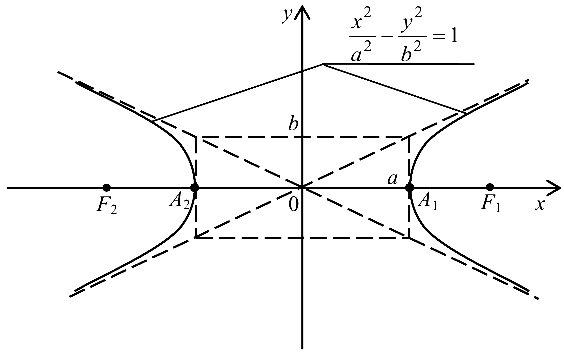
Гипербола имеет две оси симметрии (координатные оси), с одной из которых (осью абсцисс) она пересекается в двух точках 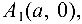
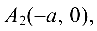 называемых вершинами гиперболы. Числа
называемых вершинами гиперболы. Числа 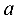 и
и 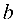 — полуоси гиперболы:
— полуоси гиперболы: 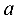 — действительная полуось,
— действительная полуось, 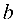 — мнимая. Точки
— мнимая. Точки 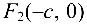 и
и 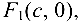 где
где 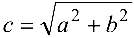 , называются фокусами гиперболы.
, называются фокусами гиперболы.
Парабола с каноническим уравнением 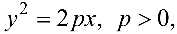 имеет форму, изображенную на рис. 4.6.
имеет форму, изображенную на рис. 4.6.
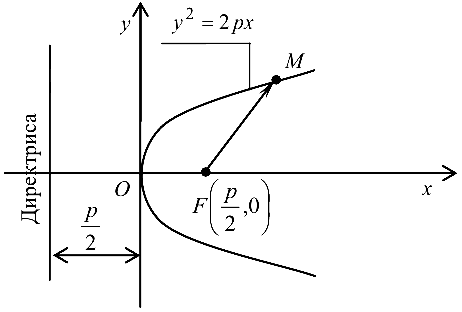
Число 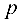 называется параметром параболы, точка
называется параметром параболы, точка 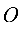 — ее вершиной, а ось
— ее вершиной, а ось 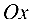 — осью параболы, вектор
— осью параболы, вектор 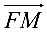 — фокальный радиус-вектор точки
— фокальный радиус-вектор точки 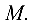 Прямая
Прямая 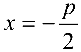 называется директрисой параболы.
называется директрисой параболы.
Задача №4.9.
Упростить уравнение 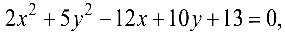 пользуясь переносом начала координат. Построить линию, определяемую этим уравнением.
пользуясь переносом начала координат. Построить линию, определяемую этим уравнением.
Решение:
Выделим полные квадраты по переменным 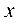 и
и 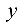 соответственно.
соответственно.
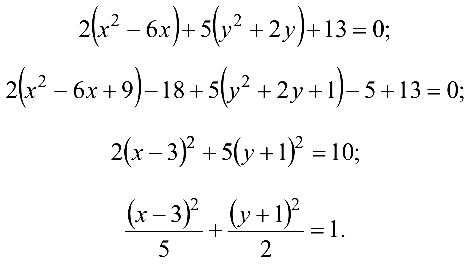
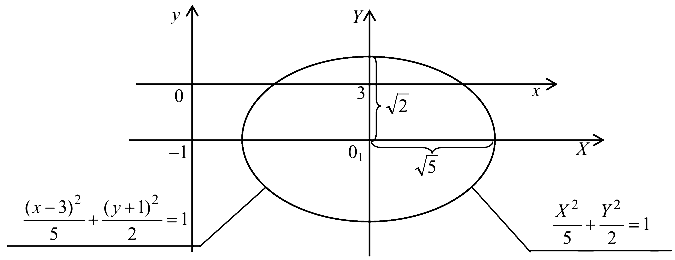
Обозначая 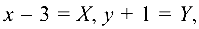 получим каноническое уравнение эллипса
получим каноническое уравнение эллипса 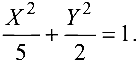 Начало новой системы координат — точка
Начало новой системы координат — точка 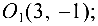 оси
оси 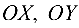 параллельны осям
параллельны осям 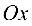 и
и 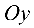 соответственно. Большая полуось эллипса
соответственно. Большая полуось эллипса 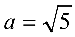 , малая полуось
, малая полуось 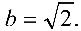 Изобразим кривую на рис. 4.7.
Изобразим кривую на рис. 4.7.
Поверхности второго порядка
Поверхностью второго порядка называется множество точек пространства, координаты 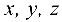 которых в прямоугольной системе координат удовлетворяют уравнению второй степени:
которых в прямоугольной системе координат удовлетворяют уравнению второй степени:
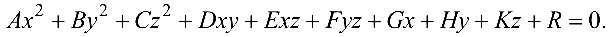
Уравнение (4.11) называется общим уравнением поверхности второго порядка (коэффициенты 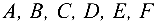 не равны нулю одновременно). Если поверхность невырожденная, то при помощи преобразования прямоугольных координат (параллельного переноса и поворота) всегда можно найти такую новую систему координат, в которой уравнение (4.11) имеет один из следующих видов (каноническое уравнение):
не равны нулю одновременно). Если поверхность невырожденная, то при помощи преобразования прямоугольных координат (параллельного переноса и поворота) всегда можно найти такую новую систему координат, в которой уравнение (4.11) имеет один из следующих видов (каноническое уравнение):
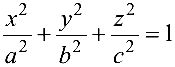 — эллипсоид; (4.12)
— эллипсоид; (4.12)
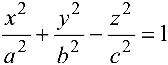 — однополостный гиперболоид; (4.13)
— однополостный гиперболоид; (4.13)
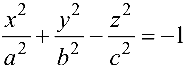 — двухполостный гиперболоид; (4.14)
— двухполостный гиперболоид; (4.14)
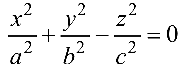 — конус: (4.15)
— конус: (4.15)
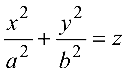 — эллиптический параболоид; (4.16)
— эллиптический параболоид; (4.16)
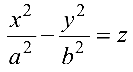 — гиперболический параболоид: (4.17)
— гиперболический параболоид: (4.17)
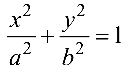 — эллиптический цилиндр; (4.18)
— эллиптический цилиндр; (4.18)
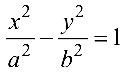 — гиперболический цилиндр; (4.19)
— гиперболический цилиндр; (4.19)
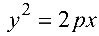 — параболический цилиндр. (4.20)
— параболический цилиндр. (4.20)
В уравнениях (4.12)-(4.20) 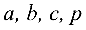 положительны.
положительны.
Задача №4.10.
Построить тело, ограниченное поверхностями 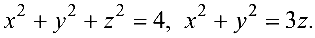
Решение:
Тело ограничено снизу поверхностью параболоида: 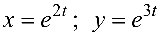 , а сверху — поверхностью сферы
, а сверху — поверхностью сферы 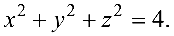
Тело изображено на рис. 4.8.
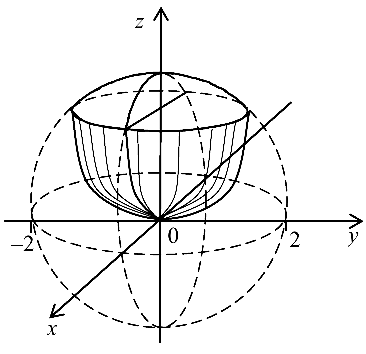
Задача №4.11.
Построить тело, ограниченное поверхностями.
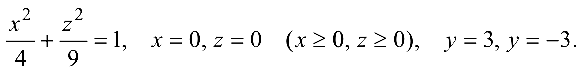
Решение:
Поверхность 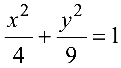 — эллиптический цилиндр.
— эллиптический цилиндр.
Он пересечен плоскостями 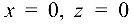 (координатные плоскости
(координатные плоскости 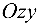 и
и 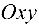 ). По оси
). По оси 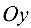 тело ограничено плоскостями
тело ограничено плоскостями 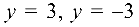 (рис. 4.9).
(рис. 4.9).
Кстати готовые на продажу задачи тут, и там же теория из учебников может быть вам поможет она.
Дополнительный материал по линейной алгебре
Линейная алгебра — это раздел математики, касающийся линейных уравнений. Линейная алгебра занимает центральное место почти во всех областях математики. Например, линейная алгебра является фундаментальной в современных представлениях геометрии, в том числе для определения основных объектов, таких как линии, плоскости и вращения.
Кроме того, функциональный анализ, раздел математического анализа, можно рассматривать как в основном применение линейной алгебры к пространствам функций.
Линейная алгебра также используется в большинстве наук и областей техники , поскольку она позволяет моделировать многие природные явления и эффективно проводить вычисления с такими моделями. Для нелинейных систем, которые не могут быть смоделированы с линейной алгеброй, он часто используются для борьбы с аппроксимациями первого порядка, используя тот факт, что дифференциал из многомерной функции в точке является линейным отображением , что лучше аппроксимирует функцию вблизи этой точки.
Матрицы. Операции над матрицами
Определение 1. Матрицей размерности 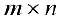 называется прямоугольная таблица из
называется прямоугольная таблица из 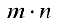 чисел, записанных в виде
чисел, записанных в виде
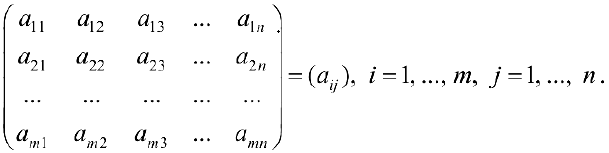
Если 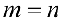 , то матрица называется квадратной порядка
, то матрица называется квадратной порядка 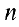 .
.
Замечание. Первый индекс в обозначении элемента — номер строки, второй — номер столбца.
Определение 2. Пусть 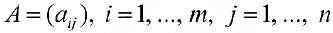 и
и 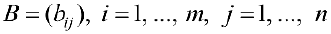 две матрицы, размерности
две матрицы, размерности 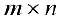 . Суммой матриц
. Суммой матриц 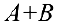 будем называть матрицу вида
будем называть матрицу вида 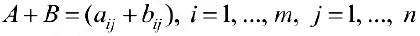 (складываются элементы, стоящие на одинаковых местах).
(складываются элементы, стоящие на одинаковых местах).
Произведением матрицы 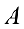 на число с будем называть матрицу
на число с будем называть матрицу 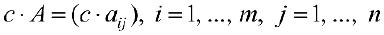 (каждый элемент матрицы
(каждый элемент матрицы 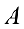 умножается на число
умножается на число 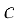 ).
).
Пример задачи №1.
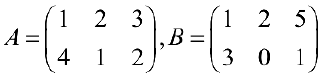
Найти 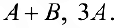
Решение:
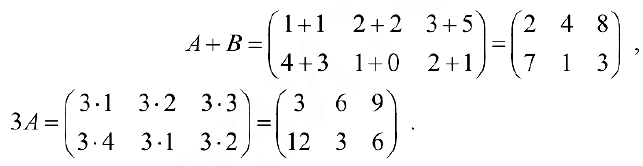
Определение 3. Пусть 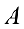 — матрица размерности
— матрица размерности 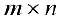 вида (1). Транспонированной матрицей к матрице
вида (1). Транспонированной матрицей к матрице 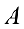 будем называть матрицу
будем называть матрицу 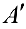 размерности
размерности 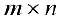 вида
вида
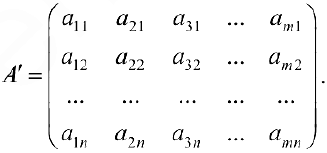
Пример задачи №2.
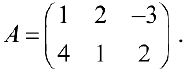 Найти
Найти 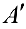 .
.
Решение:
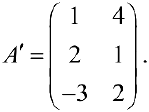
Свойства операций сложения матриц и умножения матрицы на число
Для любых матриц 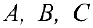 размерности
размерности 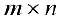 и любых действительных чисел
и любых действительных чисел 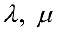 выполняются следующие 8 свойств:
выполняются следующие 8 свойств:
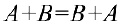 — коммутативность сложения.
— коммутативность сложения.
2. 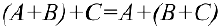 — ассоциативность сложения.
— ассоциативность сложения.
3. Существование нулевого элемента 0, обладающего свойством: 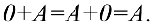 В качестве 0 берется матрица, все элементы которой равны 0.
В качестве 0 берется матрица, все элементы которой равны 0.
4. Существование противоположного элемента:  матрицы
матрицы 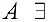 матрица
матрица 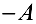 такая, что
такая, что 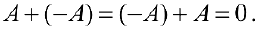 В качестве
В качестве 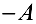 берется матрица, элементы которой противоположны по знаку соответствующим элементам матрицы
берется матрица, элементы которой противоположны по знаку соответствующим элементам матрицы 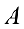 .
.
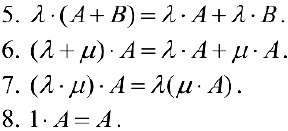
Определение 4. Пусть 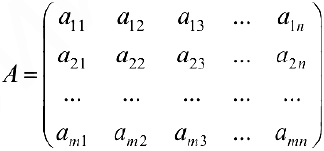 и
и 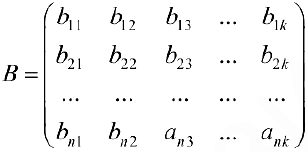 две матрицы размерности
две матрицы размерности 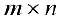 и
и 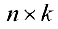 (число столбцов 1-ой матрицы равно числу строк 2-ой). Произведением матриц
(число столбцов 1-ой матрицы равно числу строк 2-ой). Произведением матриц 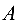 и
и 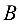 называется матрица
называется матрица 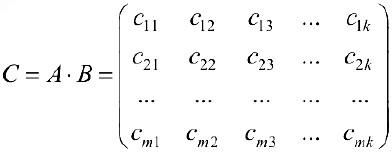 размерности
размерности 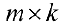 ,
,
элементы которой находятся по формуле
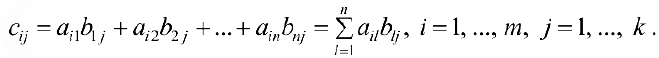
Пример задачи №3.
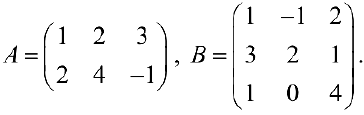 Найти
Найти 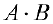 .
.
Решение:
По формуле (3):
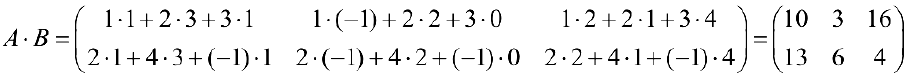
Замечание. 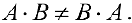
Определители матриц
Определение 5. Пусть 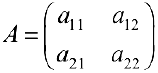 — квадратная матрица размерности
— квадратная матрица размерности 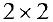 . Определителем (детерминантом) матрицы
. Определителем (детерминантом) матрицы 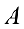 будем называть число
будем называть число
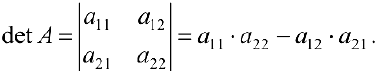
Пусть 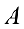 — квадратная матрица размерности
— квадратная матрица размерности
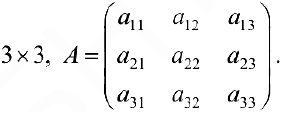
Определителем (детерминантом) матрицы 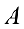 будем называть число
будем называть число 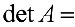
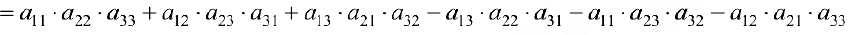
Пример задачи №4.
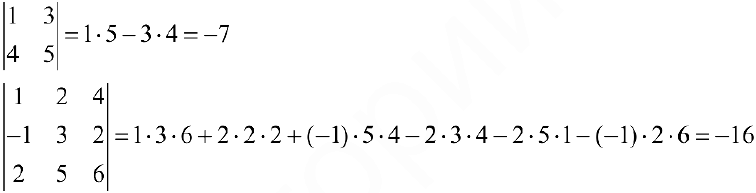
Свойства определителей
- Если какую-либо строку (столбец) матрицы
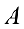 умножить на число
умножить на число 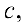 то и определитель умножится на число
то и определитель умножится на число 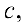 то есть определитель полученной матрицы
то есть определитель полученной матрицы 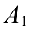 будет равен:
будет равен: 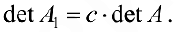
- Если переставить местами любые две строки (столбца) матрицы, то определитель поменяет знак, то есть определитель полученной матрицы
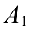 будет равен:
будет равен: 
- Если к какой-нибудь строке (столбцу) матрицы А прибавить любую другую строку (столбец) матрицы
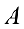 умноженной на любое число
умноженной на любое число 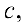 то определитель не изменится, то есть определитель полученной матрицы
то определитель не изменится, то есть определитель полученной матрицы 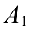 будет равен:
будет равен: 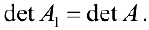
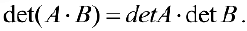
- Определитель единичной матрицы
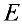 равен 1. (единичная матрица — это матрица, у которой на главной диагонали стоят 1, а все остальные элементы равны 0).
равен 1. (единичная матрица — это матрица, у которой на главной диагонали стоят 1, а все остальные элементы равны 0). - Определитель треугольной матрицы равен произведению элементов, стоящих на главной диагонали.
Замечание. Из свойств 1-5 следуют другие полезные свойства.
Следствие 1. Если строка (столбец) матрицы равны 0, то ее определитель равен 0.
Следствие 2. Если у матрицы две одинаковые строки (столбца), то ее определитель равен 0.
Пример задачи №5.
Найдем определитель из примера 4, предварительно преобразовав матрицу
- Ко второй строке матрицы прибавим первую, и к третьей строке матрицы прибавим первую, умноженную на -2, получим:
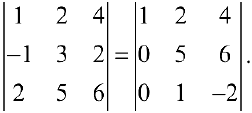
2. Переставим местами вторую и третью строки, затем к третьей прибавим вторую, умноженную на -5, получим:
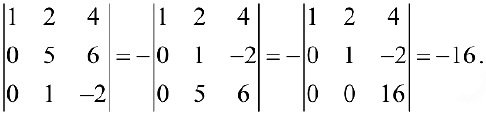
Определение 6. Пусть 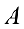 квадратная матрица порядка
квадратная матрица порядка 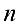 и
и 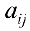 — фиксированный элемент в этой матрице. Мысленно вычеркнем
— фиксированный элемент в этой матрице. Мысленно вычеркнем 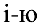 строку и
строку и 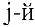 столбец из матрицы
столбец из матрицы 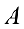 и обозначим определитель матрицы, составленной из оставшихся элементов, через
и обозначим определитель матрицы, составленной из оставшихся элементов, через 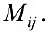 Тогда
Тогда 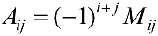 называется алгебраическим дополнением к элементу
называется алгебраическим дополнением к элементу 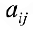 .
.
Теорема 1. Пусть 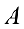 — квадратная матрица порядка
— квадратная матрица порядка 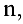
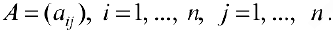 Тогда
Тогда
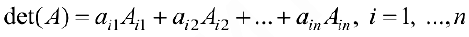
Формула (6) называется формулой разложения определителя по элементам 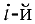 строки.
строки.
Замечание. Аналогичная формула верна для любого столбца.
Формула (6) сводит вычисления определителя 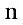 -ого порядка к вычислению определителя
-ого порядка к вычислению определителя 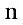 -1 порядка.
-1 порядка.
Пример задачи №6.
Вычислим определитель из примера 4. разложенного по элементам первой строки.
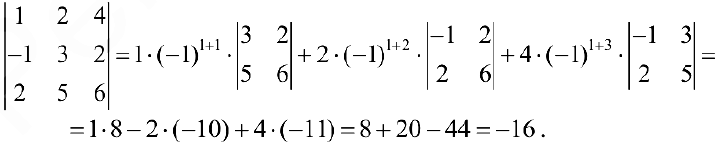
Разложим определитель по элементам 2-ого столбца.
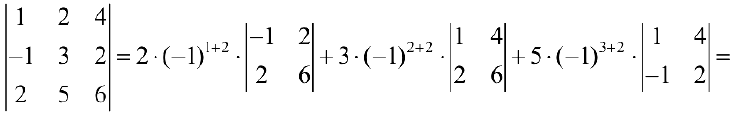
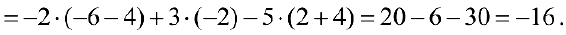
Методы вычисления определителя n — ого порядка
- Разложение по элементам строки (столбца).
В этом случае используют теорему 1 и сводят вычисление определителя порядка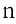 к вычислению определителя порядка
к вычислению определителя порядка 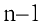 (см. пример 6).
(см. пример 6). - Приведение определителя к треугольному виду.
С помощью свойств определителя приводят матрицу к треугольному виду. Определитель полученной матрицы равен произведению элементов, стоящих на диагонали (следует из теоремы 1).
Пример задачи №7.
Вычислить определитель порядка 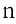 :
: 
- Прибавим к 1-ой строке все остальные строки, получим:

2. Вычтем 1 -ую строку из всех остальных строк, получим:

Упражнение 1.1. Найти матрицу 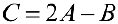 , где
, где
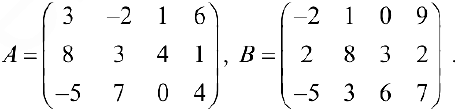
Упражнение 1.2. Даны следующие матрицы:
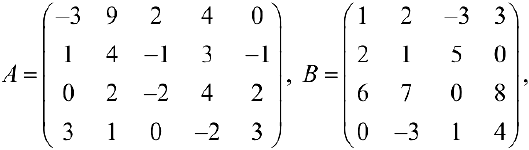
Обратная матрица
Определение 1. Пусть 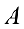 квадратная матрица размерностью
квадратная матрица размерностью  . Матрица
. Матрица 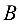 называется обратной матрицей к матрице
называется обратной матрицей к матрице 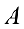 , если
, если
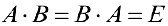 , (1)
, (1)
где 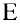 — единичная матрица.
— единичная матрица.
При этом матрица 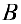 обозначается как
обозначается как 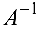 и тогда равенство (1) переписывается в следующем виде:
и тогда равенство (1) переписывается в следующем виде:
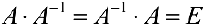 . (2)
. (2)
Теорема 1. Если обратная матрица существует. То она единственна.
Доказательство. От противного. Предположим, что для матрицы 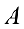 существует две неравные друг другу матрицы
существует две неравные друг другу матрицы 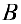 и
и 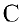 , такие, что
, такие, что
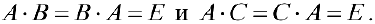
Тогда рассмотрим равенства
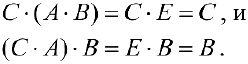
Так как левые части равенств равны, то равны и правые, то есть 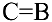 — противоречие, что и требовалось доказать.
— противоречие, что и требовалось доказать.
Теорема 2. Для матрицы 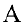 существует обратная матрица
существует обратная матрица 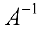 тогда и только тогда, когда определитель матрицы
тогда и только тогда, когда определитель матрицы 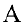 не равен 0.
не равен 0.
Доказательство.
- Необходимость. Докажем, что если для матрицы
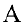 существует обратная матрица
существует обратная матрица 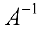 , то
, то 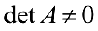 . По свойству (2):
. По свойству (2): 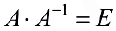 . Тогда
. Тогда 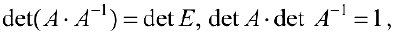 поэтому
поэтому 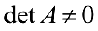 , ч.т.д.
, ч.т.д. - Достаточность. Пусть определитель
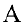 не равен 0. Докажем, что для матрицы
не равен 0. Докажем, что для матрицы 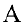 существует обратная.
существует обратная.
Рассмотрим матрицу из алгебраических дополнений к элементам матрицы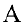 , составленную так, что алгебраические дополнения к строкам пишутся в соответствующие столбцы:
, составленную так, что алгебраические дополнения к строкам пишутся в соответствующие столбцы:
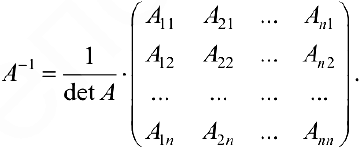
Непосредственно проверяем, что для этой матрицы выполняется равенство (2):
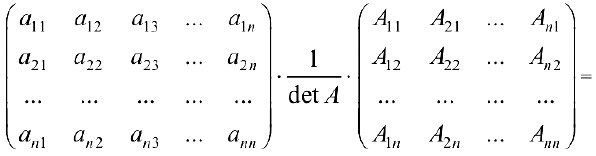

Действительно, по формуле (3) элемент 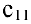 равен
равен
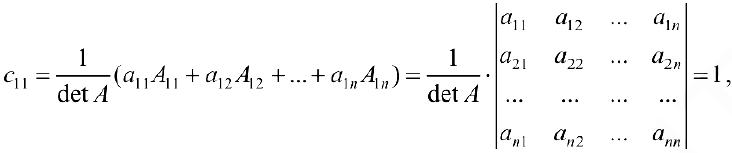
элемент 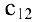 равен
равен
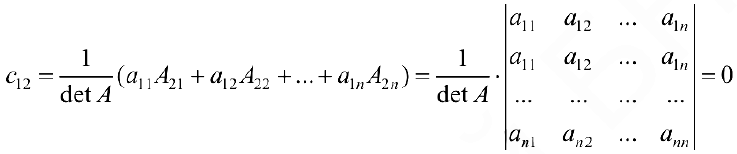
и т.д. Теорема доказана.
Пример задачи №8.
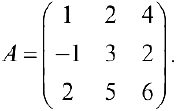 Проверить, что для матрицы существует обратная и найти ее.
Проверить, что для матрицы существует обратная и найти ее.
Решение:
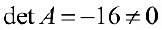 (см. пример 4), поэтому по теореме 2 матрица
(см. пример 4), поэтому по теореме 2 матрица 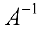 существует.
существует.
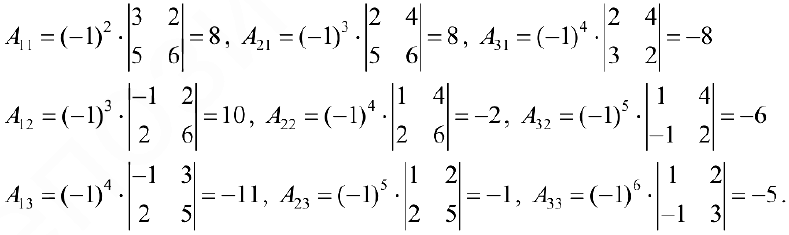
Тогда по формуле (3):
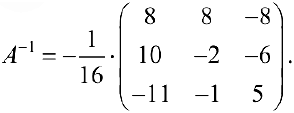
Определение 2. Система уравнений вида
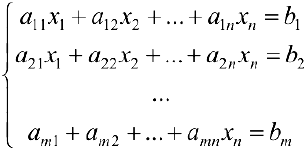
называется системой 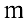 линейных уравнений с
линейных уравнений с 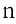 неизвестными.
неизвестными.
Матрица 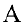 , составленная из коэффициентов при неизвестных,
, составленная из коэффициентов при неизвестных,
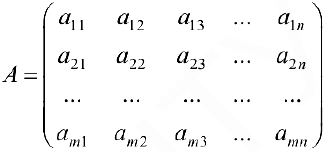
называется матрицей системы, столбец 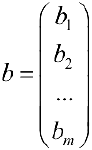 — столбцом свободных членов. При этом систему можно переписать в матричном виде:
— столбцом свободных членов. При этом систему можно переписать в матричном виде:

Совокупность чисел 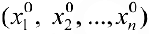 — называется решением системы (4), если при подстановке их в систему получаются верные равенства.
— называется решением системы (4), если при подстановке их в систему получаются верные равенства.
Если система (4) имеет хотя бы одно решение, она называется совместной, в противном случае — несовместной.
Теорема 3. Рассмотрим систему 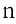 линейных уравнений с
линейных уравнений с 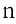 неизвестными.
неизвестными.
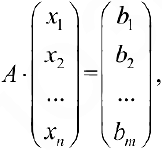
где 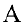 — матрица системы. Предположим, что для матрицы
— матрица системы. Предположим, что для матрицы 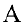 существует обратная матрица. Тогда система (6) имеет единственное решение
существует обратная матрица. Тогда система (6) имеет единственное решение
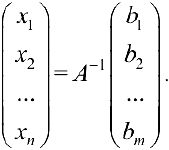
Доказательство. Умножим обе части равенства (6) на 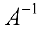 :
:
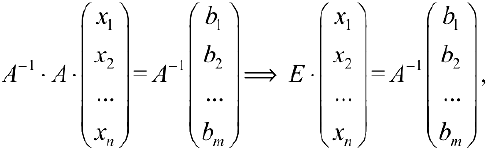
поэтому 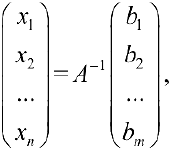 ч.т.д.
ч.т.д.
Замечание. Решение системы по формуле (7) называется матричным методом решения системы. Из формул (7) и (3) следует:
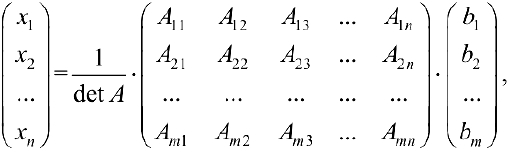
тогда
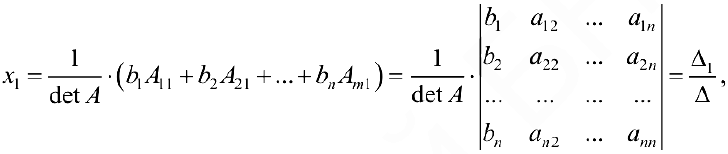
где через  обозначен определитель матрицы
обозначен определитель матрицы 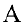 системы, а
системы, а 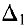 — определитель матрицы, полученной из матрицы
— определитель матрицы, полученной из матрицы 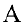 заменой первого столбца столбцом свободных членов. Аналогично,
заменой первого столбца столбцом свободных членов. Аналогично, 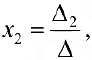 где
где 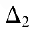 — определитель матрицы,
— определитель матрицы, 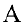 полученной из матрицы А заменой второго столбца столбцом свободных членов и т.д.
полученной из матрицы А заменой второго столбца столбцом свободных членов и т.д.
Полученные формулы называются формулами Крамера.
Пример задачи №9.
Решить систему уравнений 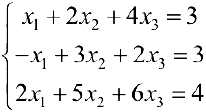
1) матричным способом; 2) по формулам Крамера.
Решение:
1) Матричный способ. Перепишем систему в матричном виде:
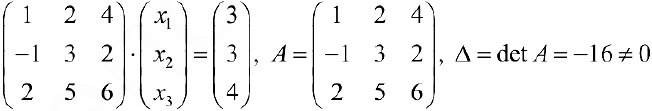
(см. пример 4), поэтому обратная матрица существует и решение системы единственно.
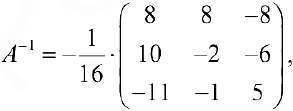 (см пример 1), тогда по формуле (7)
(см пример 1), тогда по формуле (7)
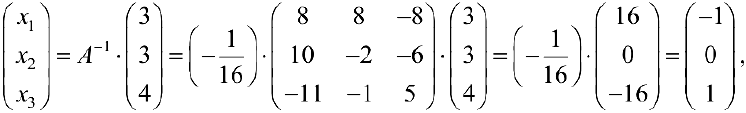
то есть 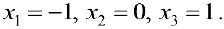
2) Формулы Крамера. 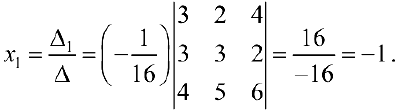
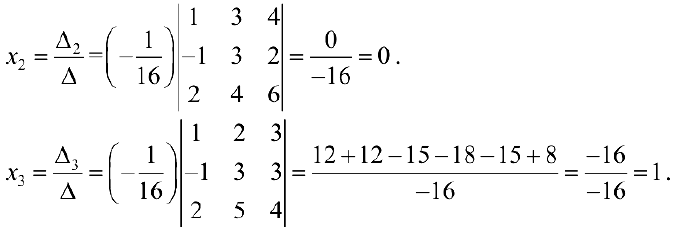
Замечание. Если рассмотреть матричное уравнение 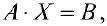 (8) где
(8) где 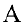 и
и 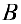 данные матрицы, а
данные матрицы, а 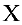 — неизвестная матрица, то, рассуждая аналогично теореме 3, получим формулу:
— неизвестная матрица, то, рассуждая аналогично теореме 3, получим формулу:
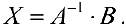 (9)
(9)
Аналогично, для матричного уравнения
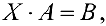 (10)
(10)
получим формулу:
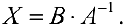 (11)
(11)
Пример задачи №10.
Решить матричное уравнение 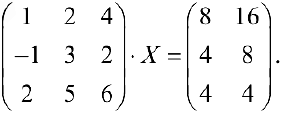
Решение:
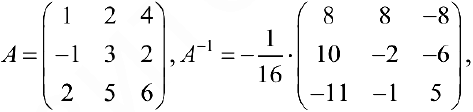
(см. пример 1), тогда по формуле (9):
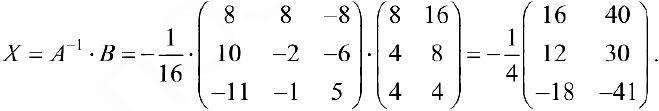
Упражнение 2.1. Найдите обратные матрицы для заданных матриц:
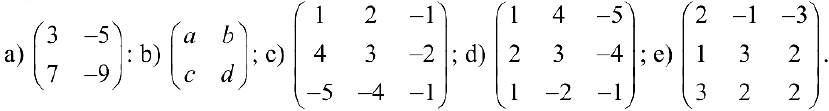
Упражнение 2.2. Выяснить при каких значениях 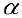 существует матрица, обратная данной.
существует матрица, обратная данной.
Ранг матрицы
Определение 1. Пусть 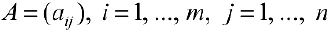 произвольная матрица размерности
произвольная матрица размерности 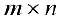 . Выберем в матрице
. Выберем в матрице 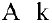 строк
строк 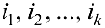 и
и 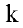 столбцов
столбцов 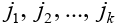 и обозначим через
и обозначим через
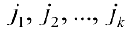
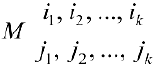 определитель матрицы размерности
определитель матрицы размерности 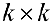 , составленный из элементов матрицы
, составленный из элементов матрицы 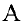 , стоящих на пересечении выбранных строк и столбцов.
, стоящих на пересечении выбранных строк и столбцов.
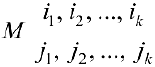 называется минором порядка
называется минором порядка 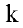 .
.
Пример задачи №11.
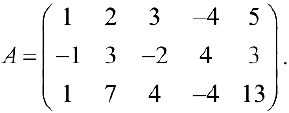 Найдем миноры
Найдем миноры 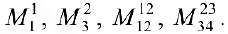
Решение:
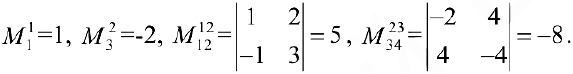
Определение 2. Рангом матрицы называется наибольший из порядков миноров, отличных от нуля. Ранг будем обозначать через 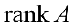 или
или 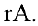 Не равный нулю минор, порядок которого равен рангу матрицы, называется базисным минором.
Не равный нулю минор, порядок которого равен рангу матрицы, называется базисным минором.
Замечание. Не обязательно перебирать все миноры матрицы, чтобы найти ее ранг.
Оказывается, для этого достаточно рассматривать вложенные друг в друга миноры. На этом основывается, так называемый, метод окаймляющих миноров.
Для нахождения ранга матрицы проводят настолько долго, насколько это возможно следующие операции.
- Рассматривают миноры 1-ого порядка. Если все они равны 0, то
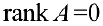 и конец алгоритма.
и конец алгоритма.
Если хотя бы одни из них не равен 0, то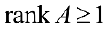 и переходят на п.2.
и переходят на п.2. - Рассматривают все миноры 2-ого порядка, окаймляющие фиксированный ненулевой минор 1-ого порядка. Если все они равны 0, то
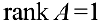 и конец алгоритма.
и конец алгоритма.
Если хотя бы один из них не равен 0, то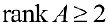 и переходят па рассмотрение миноров 3-ого порядка, окаймляющих фиксированный ненулевой минор 2-ого порядка, и т.д., пока есть что окаймлять.
и переходят па рассмотрение миноров 3-ого порядка, окаймляющих фиксированный ненулевой минор 2-ого порядка, и т.д., пока есть что окаймлять.
Пример задачи №12.
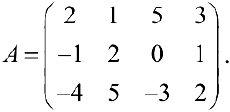
Найти ранг 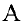 методом окаймляющих миноров.
методом окаймляющих миноров.
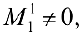 поэтому
поэтому 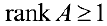 . Рассмотрим минор
. Рассмотрим минор 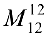 , окаймляющий
, окаймляющий 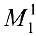 .
.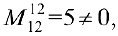 поэтому
поэтому 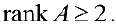
- Минор
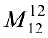 окаймляют два минора третьего порядка
окаймляют два минора третьего порядка 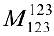 и
и 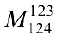 .
.
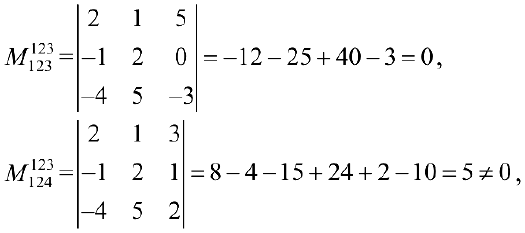
поэтому 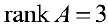 .
.
Определение 3. Элементарными преобразованиями матрицы называются:
1) перестановка любых 2-х строк (столбцов) матрицы;
2) умножение любой строки (столбца) матрицы на отличное от нуля число;
3) прибавление к любой строке (столбцу) матрицы любой другой строки (столбца) матрицы, умноженных на произвольное число.
Теорема 1. Элементарные преобразования матрицы не изменяют ее ранга. С помощью элементарных преобразований любую матрицу 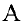 можно привести к трапециевидному виду:
можно привести к трапециевидному виду:
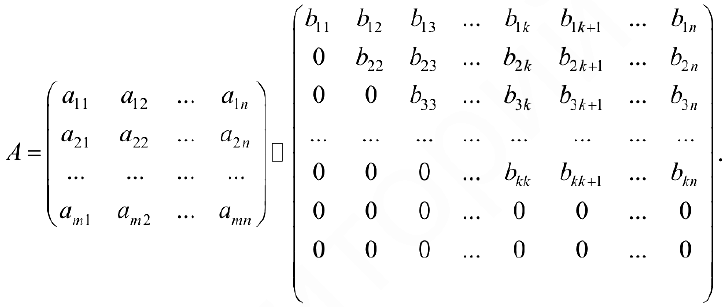
Где все строки, начиная с 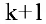 — ой равны 0, а элементы стоящие на диагонали
— ой равны 0, а элементы стоящие на диагонали 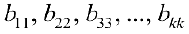 не равны 0. И тогда ранг матрицы равен
не равны 0. И тогда ранг матрицы равен 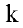 .
.
Пример задачи №13.
С помощью элементарных преобразований найти ранг матрицы 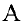 и базисный минор,
и базисный минор,
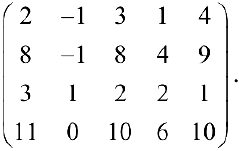
Решение:
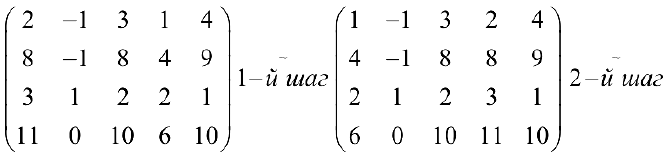
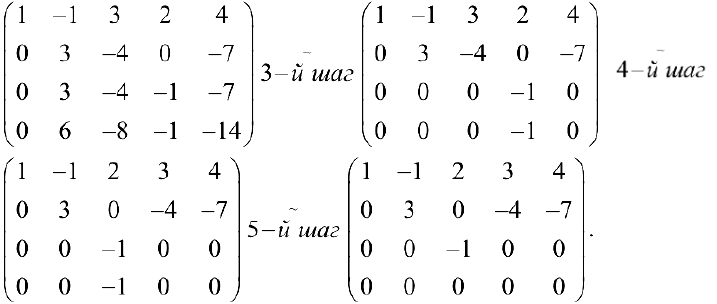
1- й шаг. Меняем местами 1-й и 4-й столбцы.
2- й шаг. Ко второй, третьей и четвертой строкам прибавляем первую, умноженную соответственно на -4, -2, -6.
3- й шаг. К третьей и четвертой строкам прибавляем вторую, умноженную соответственно на -1,-2.
4- й шаг. Меняем местами 3-й и 4-й столбцы.
5- й шаг. К четвертому столбцу прибавляем третий, умноженный на -1.
В результате получаем матрицу трапециевидного вида из теоремы 1. Тогда 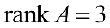 , базисный минор в первоначальной матрице:
, базисный минор в первоначальной матрице: 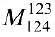 , так как в результате двух перестановок столбцов первый столбец оказался па третьем месте, а четвертый — на первом.
, так как в результате двух перестановок столбцов первый столбец оказался па третьем месте, а четвертый — на первом.
Упражнение 3.1. Найти миноры 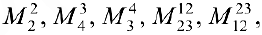
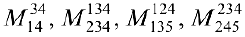 указанных матрицах:
указанных матрицах:
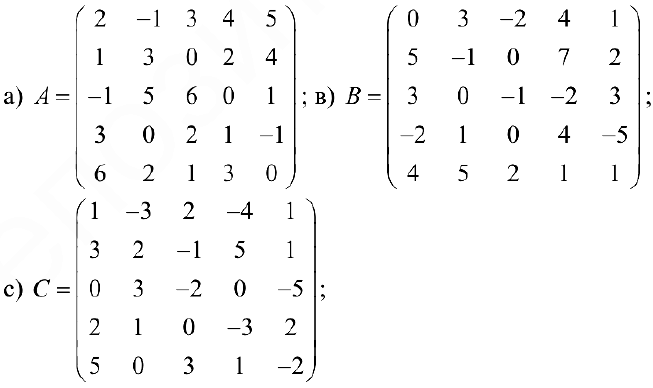
Ответы:
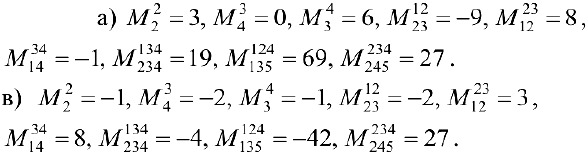
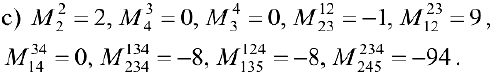
Упражнение 3.2. Найти ранг матрицы методом окаймляющих миноров:

Ответы: а) 3; в) 3; с) 2.
Упражнение 3.3. Найти ранг матрицы с помощью элементарных преобразований:

Ответы: а) 4; в) 4; с) 4; d) 3.
Упражнение 3.4. Найти ранг матрицы в зависимости от значений параметра 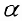 ;
;
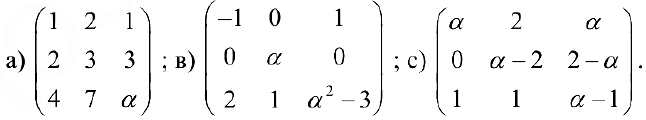
При каких значениях 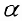 матрица имеет обратную?
матрица имеет обратную?
Решение произвольных систем линейных уравнений
Рассмотрим систему 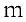 линейных уравнений с
линейных уравнений с 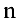 неизвестными вида:
неизвестными вида:
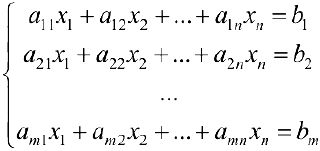
или в матричном виде
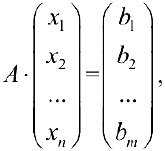
где 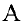 — матрица системы. При этом матрица
— матрица системы. При этом матрица 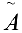 вида
вида 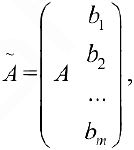 которая получается, если к матрице
которая получается, если к матрице 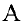 справа добавить столбец свободных членов, называется расширенной матрицей системы.
справа добавить столбец свободных членов, называется расширенной матрицей системы.
Теорема (Кронекера-Капелли)
Для того, чтобы система уравнений (1) имела решение необходимо и
достаточно, чтобы 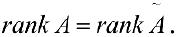
Докажем необходимость. Дано: система имеет решение. Докажем, что 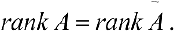 Пусть
Пусть 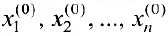 — решение системы. Тогда при подстановке этих чисел в систему получим верные равенства. Запишем эти равенства в векторном виде:
— решение системы. Тогда при подстановке этих чисел в систему получим верные равенства. Запишем эти равенства в векторном виде:
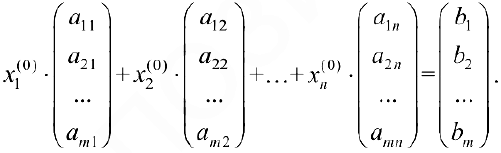
Рассмотрим матрицу 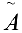 . Вычтем из последнего столбца первый, умноженный на
. Вычтем из последнего столбца первый, умноженный на 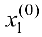 , второй — умноженный на
, второй — умноженный на  — умноженный на
— умноженный на 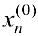 . Из (3) следует, что в результате такого преобразования получим:
. Из (3) следует, что в результате такого преобразования получим:
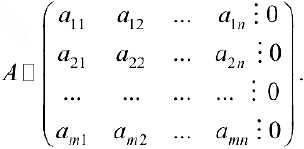
Поэтому 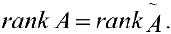
Замечание. Теорема 1 дает конкретный алгоритм решения произвольных систем:
- Находят
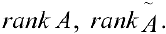 Если они не равны, то система не имеет решений.
Если они не равны, то система не имеет решений. - Если они равны, рассматриваем базисный минор матрицы
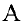 . Все уравнения, нс входящие в базисный минор отбрасывают. Неизвестные в оставшихся уравнениях, не входящие в базисный минор, переносят направо и полученную систему решают по правилам Крамера или матричным методом.
. Все уравнения, нс входящие в базисный минор отбрасывают. Неизвестные в оставшихся уравнениях, не входящие в базисный минор, переносят направо и полученную систему решают по правилам Крамера или матричным методом.
При этом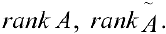 можно находить одновременно методом элементарных преобразований, если последний столбец матрицы
можно находить одновременно методом элементарных преобразований, если последний столбец матрицы 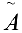 не прибавлять к другим столбцам и не переставлять его с другими.
не прибавлять к другим столбцам и не переставлять его с другими.
Пример задачи №14.
Решить систему: 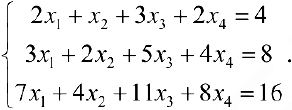
Решение:
Найдем 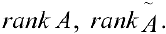

1 — й шаг. Переставляем местами 1-й и 2-й столбцы матрицы.
2 — й шаг. Ко второй и третьей строке прибавляем первую, умноженную на -2 и -4 соответственно.
3 — й шаг. От третьей строки отнимаем вторую, 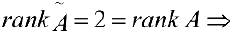 система совместна.
система совместна.
Базисный минор находится в 1, 2 столбце и 1, 2 строке. Отбрасываем 3-е уравнение. Переменные 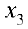 и
и 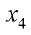 в оставшихся уравнениях переносим направо (
в оставшихся уравнениях переносим направо (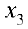 и
и 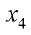 — свободные неизвестные).
— свободные неизвестные).
В результате получим систему: 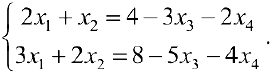
Решим ее по Правилу Крамера:
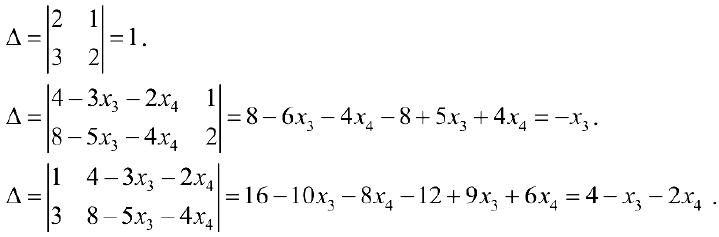
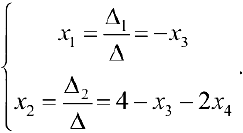
Таким образом: 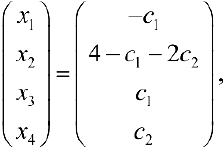 где
где 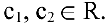
Метод Гаусса
Если при нахождении ранга матриц 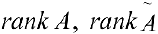 использовать только элементарные преобразования строк или перестановку столбцов, не переставляя столбец свободных членов с другими, то нет необходимости возвращаться к первичной матрице.
использовать только элементарные преобразования строк или перестановку столбцов, не переставляя столбец свободных членов с другими, то нет необходимости возвращаться к первичной матрице.
Алгоритм метода Гаусса
- Прямой ход метода Гаусса. Элементарными преобразованиями матрица
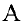 приводится к виду:
приводится к виду:
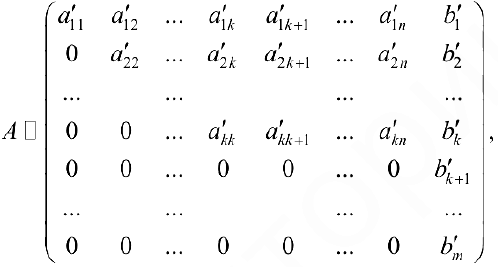
где 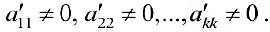 Если хотя бы один из элементов
Если хотя бы один из элементов 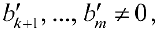 то система не имеет решений. Если же
то система не имеет решений. Если же 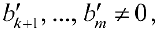 то система имеет решение и начинают обратный ход.
то система имеет решение и начинают обратный ход.
Обратный ход метода Гаусса
Рассмотрим последнее 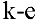 уравнение и из него выражаем
уравнение и из него выражаем 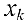 через все остальные неизвестные. Подставляем найденные
через все остальные неизвестные. Подставляем найденные 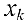 во все остальные уравнения и из
во все остальные уравнения и из 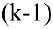 — ого уравнения выражают переменную
— ого уравнения выражают переменную 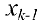 через остальные и т.д., пока не дойдем до первого уравнения.
через остальные и т.д., пока не дойдем до первого уравнения.
Пример задачи №15.
Решить систему по методу Гаусса.
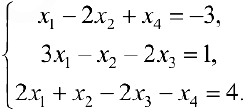
Решение:
Прямой ход метода Гаусса:
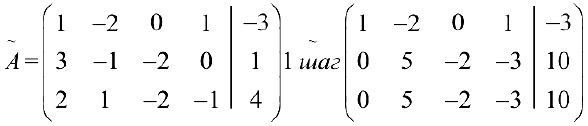
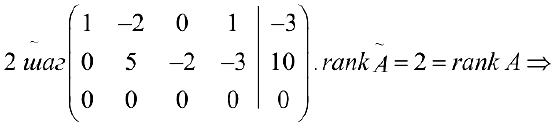
система совместна. Обратный ход метода Гаусса:
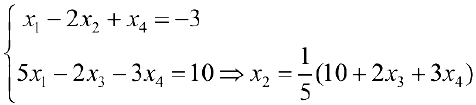
Из первого уравнения
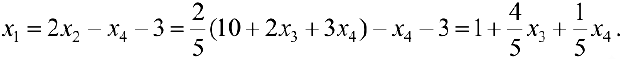
Пусть 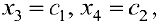 тогда
тогда 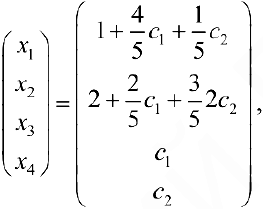 где
где 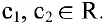
Упражнение 4.1. Исследовать данную систему и в случае совместности решить её.
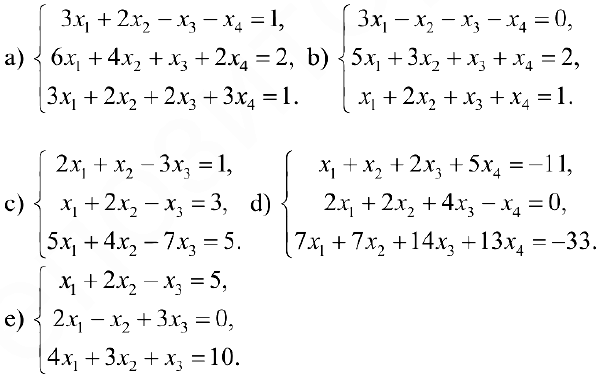
Ответы: 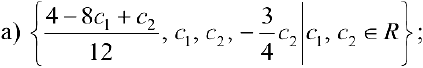
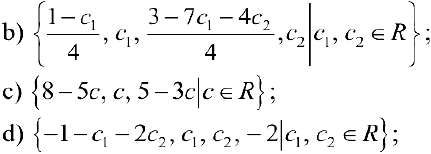
Линейные векторные пространства
Определение 1. Произвольное множество  будем называть линейным векторным пространством, если на
будем называть линейным векторным пространством, если на 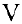 определена операция сложения его элементов (векторов), а именно:
определена операция сложения его элементов (векторов), а именно: 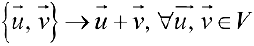 и операция умножения
и операция умножения
вектора на действительное число 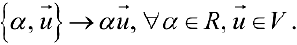 При этом необходимо, чтобы выполнялись следующие 8 аксиом:
При этом необходимо, чтобы выполнялись следующие 8 аксиом:
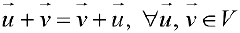 коммутативность сложения векторов.
коммутативность сложения векторов.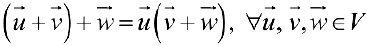 — ассоциативность сложения векторов.
— ассоциативность сложения векторов.- Существование нулевого элемента
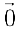 :
: 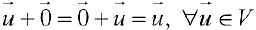 .
. - Существование противоположного элемента:
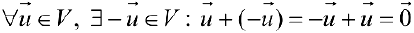 .
. 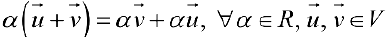 .
.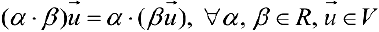 .
.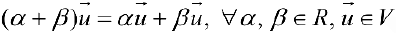 .
.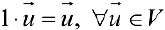 .
.
Пример задачи 1. Множество действительных чисел 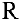 с обычными операциями сложения и умножения чисел будет линейным векторным пространством (все 8 аксиом выполняются).
с обычными операциями сложения и умножения чисел будет линейным векторным пространством (все 8 аксиом выполняются).
Пример задачи 2. Множество 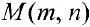 всех матриц размерности
всех матриц размерности 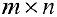 с обычными операциями сложения и умножения матрицы на число будет линейным векторным пространством (все 8 аксиом выполняются).
с обычными операциями сложения и умножения матрицы на число будет линейным векторным пространством (все 8 аксиом выполняются).
Пример задачи 3. Множество матриц вида:
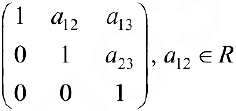 — не будет линейным векторным пространством, так как это множество не замкнуто относительно операции сложения и умножения (сумма двух элементов данного вида не будет элементом данного вида).
— не будет линейным векторным пространством, так как это множество не замкнуто относительно операции сложения и умножения (сумма двух элементов данного вида не будет элементом данного вида).
Пример задачи 4. Множество матриц вида
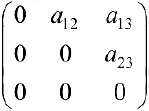 будет линейным векторным пространством.
будет линейным векторным пространством.
Пример задачи 5. Арифметическое пространство 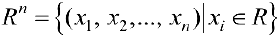 будет линейным векторным пространством, если задать операции сложения его элементов
будет линейным векторным пространством, если задать операции сложения его элементов 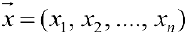 и
и 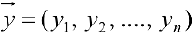 :
: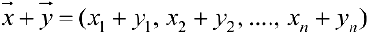 и операцию умножения на число
и операцию умножения на число 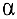 :
: 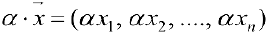 (все 8 аксиом выполняются).
(все 8 аксиом выполняются).
Определение 2. Векторы 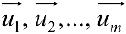 называются линейно-зависимыми, если
называются линейно-зависимыми, если 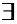 такие числа
такие числа 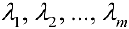 не все равные нулю, что
не все равные нулю, что
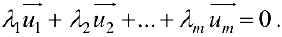
Если же равенство (1) выполняется только при нулевых значениях 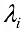
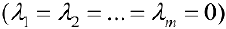 то векторы называются линейно-независимыми.
то векторы называются линейно-независимыми.
Базисом пространства 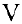 называется совокупность векторов
называется совокупность векторов 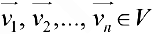 , если : 1) они линейно-независимы; 2) любой вектор
, если : 1) они линейно-независимы; 2) любой вектор 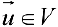 выражается через базис с какими-то координатами:
выражается через базис с какими-то координатами:
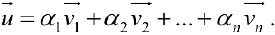
При этом числа 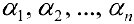 в (2) называются координатами вектора
в (2) называются координатами вектора 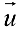 в базисе
в базисе 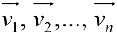 . Число
. Число 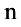 векторов базиса называется размерностью пространства
векторов базиса называется размерностью пространства 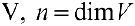 .
.
Пример задачи 6. Для линейного пространства 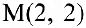 всех матриц размерности
всех матриц размерности 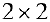 (см.пример 2) матрицы
(см.пример 2) матрицы 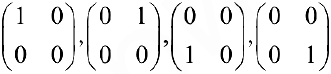 являются базисом, при этом любая матрица
являются базисом, при этом любая матрица
Для линейного пространства 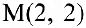 всех матриц размерности
всех матриц размерности 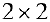 (см.пример 2) матрицы
(см.пример 2) матрицы 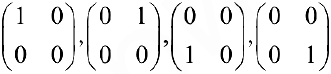 являются базисом, при этом любая матрица
являются базисом, при этом любая матрица
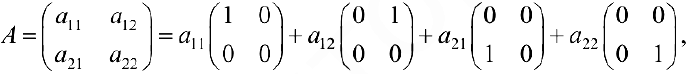
то есть координатами 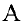 в данном базисе будут числа
в данном базисе будут числа 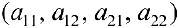 .
.
Теорема 1. Координаты вектора в данном базисе определены однозначно.
Доказательство. От противного. Предположим, что 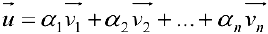 и
и 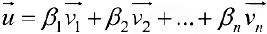 — два различных выражения вектора
— два различных выражения вектора 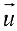 через базис. Тогда
через базис. Тогда
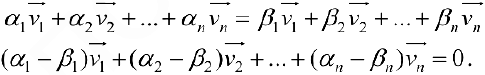
Векторы образующие базис, линейно-независимы, поэтому из (3) следует: 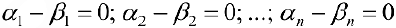 , то есть
, то есть 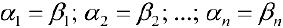 . Противоречие, что и требовалось доказать.
. Противоречие, что и требовалось доказать.
Теорема 2. Система векторов
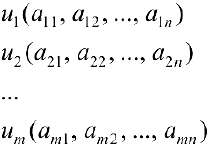 заданных своими координатами в некотором базисе, будет линейно независимой тогда и только тогда, когда ранг матрицы, составленный из координат векторов равна
заданных своими координатами в некотором базисе, будет линейно независимой тогда и только тогда, когда ранг матрицы, составленный из координат векторов равна 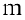 — числу векторов.
— числу векторов.
Доказательство. Достаточность. Дано: ранг матрицы равен 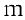 . Докажем, что векторы линейно-независимы. От противного. Предположим, что векторы линейно-зависимы. Тогда один из них линейно выражается через остальные. Например
. Докажем, что векторы линейно-независимы. От противного. Предположим, что векторы линейно-зависимы. Тогда один из них линейно выражается через остальные. Например 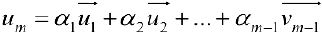 и если от последней строки отнять первую, умноженную на
и если от последней строки отнять первую, умноженную на 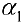 , вторую — умноженную на
, вторую — умноженную на 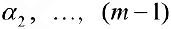 — ю умноженную
— ю умноженную 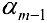 , то получим нулевую строку, то есть ранг
, то получим нулевую строку, то есть ранг 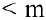 . Противоречие, ч. т. д.
. Противоречие, ч. т. д.
Пример задачи №16.
Даны векторы 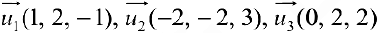 . Доказать, что они образуют базис в пространстве
. Доказать, что они образуют базис в пространстве 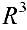 и найти в этом базисе координаты вектора
и найти в этом базисе координаты вектора 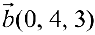 .
.
Решение:
Применим теорему 2. Найдем ранг матрицы 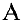 , составленной из координат векторов:
, составленной из координат векторов: 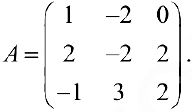 Координаты векторов выпишем в столбцы.
Координаты векторов выпишем в столбцы.
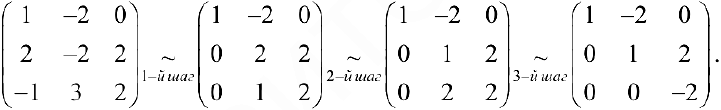
1- й шаг. Ко второй строке прибавляем первую, умноженную третьей строке прибавляем первую.
2- й шаг. Переставляем местами 2-ю и 3-ю строки.
3- й шаг. К третьей строке прибавляем вторую, умноженную на -2. 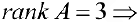 векторы линейно-независимы.
векторы линейно-независимы.
Три линейно-независимых вектора трехмерного пространства образуют базис. Найдем координаты вектора 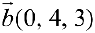 в базисе
в базисе 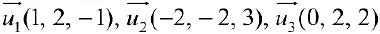 :
:
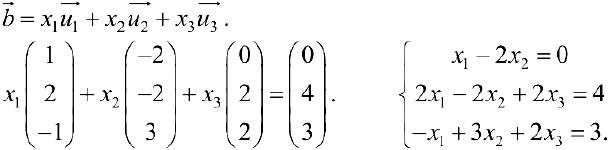
Решая систему, получим 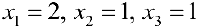 .
.
Рассмотрим однородную систему линейных уравнений:
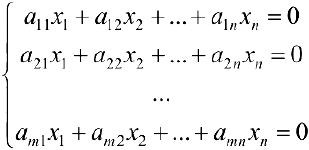
или в матричном виде 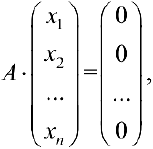 где
где 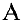 — матрица системы.
— матрица системы.
Теорема 3. Система (4) всегда совместна. Множество решений системы (4) образует линейное пространство.
Доказательство. 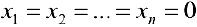 является решением системы, поэтому она совместна. Пусть
является решением системы, поэтому она совместна. Пусть 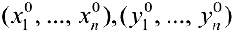 — решения системы, тогда
— решения системы, тогда 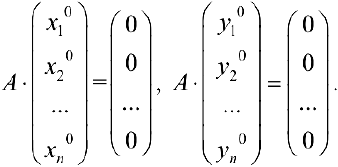 Рассмотрим вектор
Рассмотрим вектор 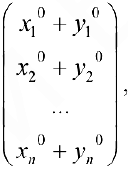 тогда
тогда 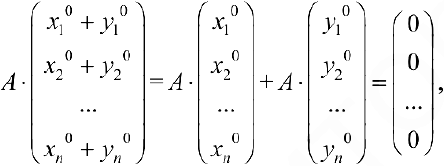 то есть вектор
то есть вектор 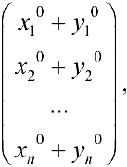 также является решением системы (4) (множество всех решений замкнуто относительно операции сложения).
также является решением системы (4) (множество всех решений замкнуто относительно операции сложения).
Аналогично доказывается, что 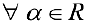
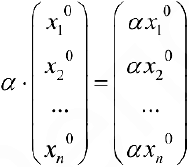 — решение системы (4). Значит множество всех решений системы замкнуто относительно операции умножения решений на число. Все 8 аксиом линейного пространства проверяются непосредственно, ч.т.д.
— решение системы (4). Значит множество всех решений системы замкнуто относительно операции умножения решений на число. Все 8 аксиом линейного пространства проверяются непосредственно, ч.т.д.
Определение . Базис пространства всех решений системы (4) называется фундаментальной системой решений.
Пример задачи №17.
Найти фундаментальную систему решений:
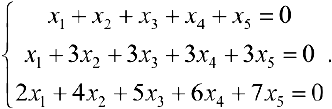
Решение:
Решим систему по методу Гаусса.
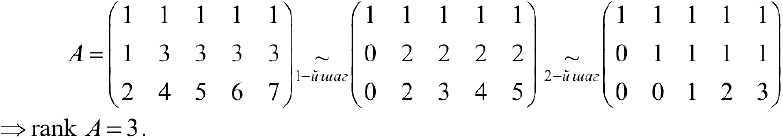
1- й шаг. Ко второй и третьей строкам прибавляем первую умноженную соответственно на -1 и -2.
2- й шаг. К третьей строке прибавляем вторую, умноженную на -1. Вторую строку сокращаем на 2.
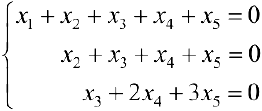
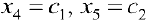 . Из последнего уравнения
. Из последнего уравнения 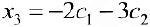 .
.
Из второго уравнения 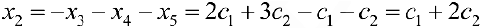 . Из первого уравнения
. Из первого уравнения 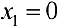 .
.
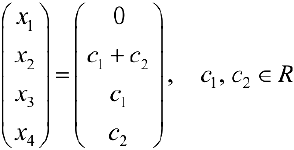 — общее решение. Количество свободных неизвестных задает размерность пространства решений.
— общее решение. Количество свободных неизвестных задает размерность пространства решений.
Для того, чтобы получить фундаментальную систему решений, одно из свободных неизвестных приравнивают к 1 остальные берут равными 0.
И так поступают со всеми свободными неизвестными по очереди.
В результате получают векторы фундаментальной системы решений.
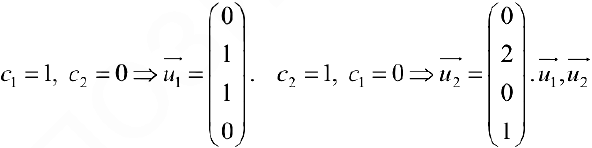 — фундаментальная система решений. При этом общее решение:
— фундаментальная система решений. При этом общее решение:
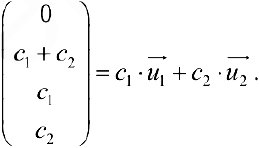
Упражнение 5.1. Даны векторы 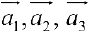 . Доказать, что они образуют базис в пространстве
. Доказать, что они образуют базис в пространстве 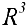 и найти в этом базисе координаты вектора
и найти в этом базисе координаты вектора 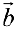 .
.
Метод Жордана — Гаусса
Рассмотрим систему уравнений. Решение систем по методу Жордана-Гаусса аналогично решению системы по методу Гаусса. При решении систем проводят элементарные преобразования строк в расширенной матрице системы. При этом, выбрав разрешающий элемент 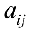 в
в 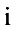 — ой строке, обнуляют, с помощью элементарных преобразований, все остальные элементы в
— ой строке, обнуляют, с помощью элементарных преобразований, все остальные элементы в 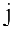 — ом столбце.
— ом столбце.
Алгоритм метода Жордана-Гаусса.
- Выписываем расширенную матрицу
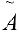 системы и в первой строке среди первых
системы и в первой строке среди первых 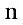 элементов находим ненулевой элемент ( например
элементов находим ненулевой элемент ( например 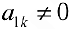 ). Делим 1-ю строку на
). Делим 1-ю строку на 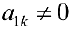 . Проведя элементарные преобразования строк, обнуляем остальные элементы
. Проведя элементарные преобразования строк, обнуляем остальные элементы 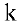 -ого столбца.
-ого столбца. - Во второй строке полученной матрицы находим среди первых
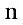 элементов ненулевой элемент
элементов ненулевой элемент 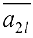 . Проводя элементарные преобразования строк, обнуляем все остальные элементы
. Проводя элементарные преобразования строк, обнуляем все остальные элементы 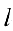 — ого столбца и т. д.
— ого столбца и т. д.
Если по ходу алгоритма получаем строки содержащие нули в первых 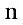 столбцах, опускаем их в конец матрицы. В результате преобразований матрица
столбцах, опускаем их в конец матрицы. В результате преобразований матрица 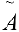 сведется к виду:
сведется к виду:
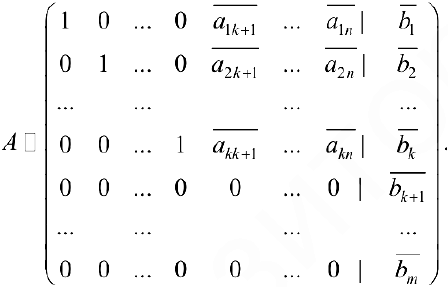
Если хотя бы одно из чисел 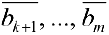 не равно нулю, то система не имеет решений. Если
не равно нулю, то система не имеет решений. Если 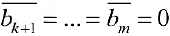 , то система имеет решение. При этом
, то система имеет решение. При этом 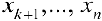 объявляют свободными неизвестными и переменные
объявляют свободными неизвестными и переменные 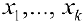 выражают через свободные неизвестные. Свободные неизвестные в системе часто будут равными пулю.
выражают через свободные неизвестные. Свободные неизвестные в системе часто будут равными пулю.
В результате получают частное (базисное решение) 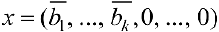 .
.
Кстати готовые на продажу задачи тут, и там же теория из учебников может быть вам поможет она.
Пример задачи №18.
Найти все базисные решения системы
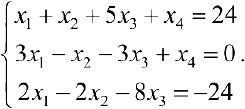
Решение:
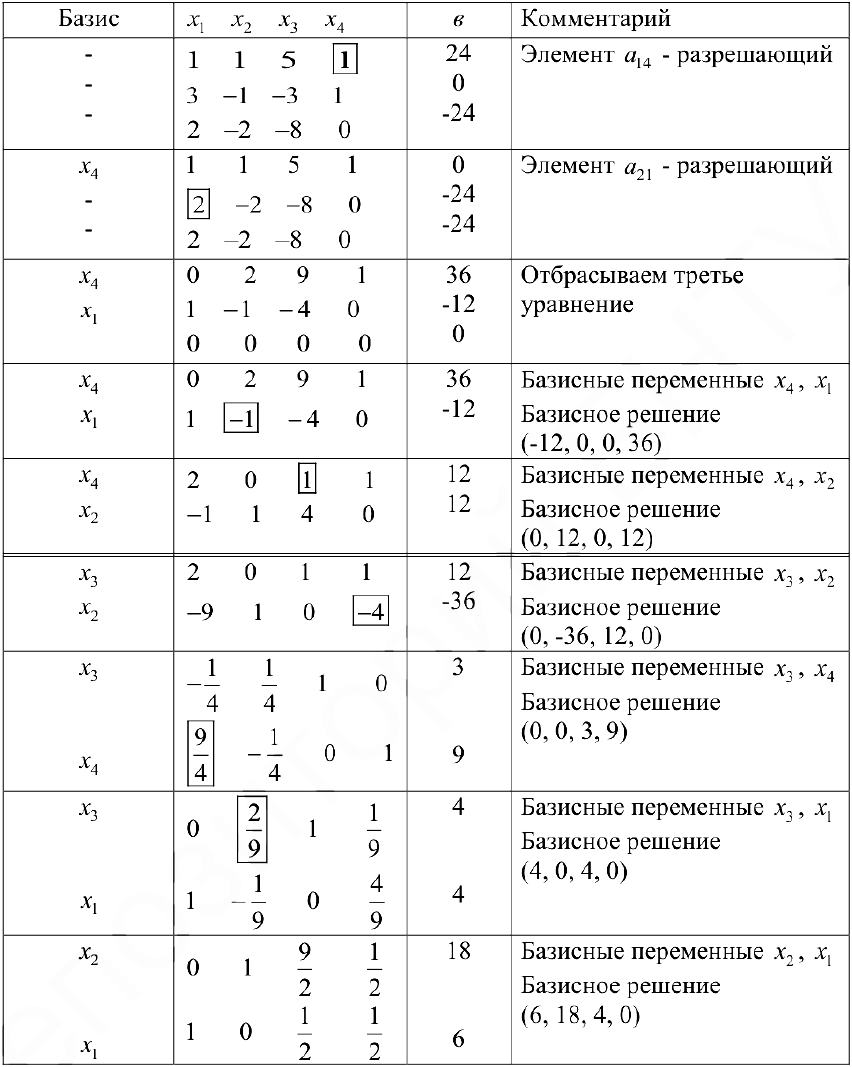
Линейная алгебра — задания и задачи с примерами решения
При изучении линейной алгебры вы познакомитесь на
примерах с понятиями линейного (векторного) пространства, линейного оператора, его матрицы, образа, ядра, ранга, дефекта, собственных векторов и собственных значений. Вы научитесь выполнять различные операции с операторами и матрицами, исследовать и решать системы линейных уравнений, получать всю информацию об операторе (матрицу, образ, ядро, ранг и дефект, собственные векторы и собственные значения) по его матрице, преобразовывать векторы и матрицы при изменениях базисов.
Правило Крамера
Постановка задачи. Решить систему трех линейных уравнений с тремя неизвестными
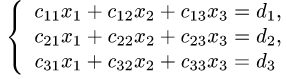
по правилу Крамера.
План решения. Если определитель матрицы системы

отличен от нуля, то система имеет решение и притом только одно.
Это решение определяется формулами
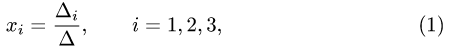
где 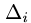 — определитель матрицы, получаемой из матрицы системы
— определитель матрицы, получаемой из матрицы системы
заменой i-ого столбца столбцом свободных членов.
1.Вычисляем определитель матрицы системы

и убеждаемся, что он не равен нулю. Следовательно система уравнений имеет единственное решение.
2.Вычисляем определители
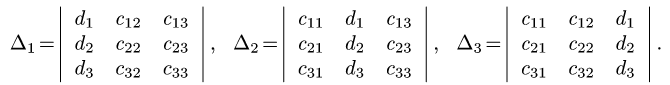
3.По формулам Крамера (1) находим решение системы уравнений
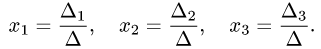
Пример. Решить систему уравнений
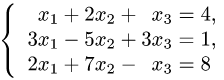
по правилу Крамера.
Решение.
1. Вычисляем определитель матрицы системы, разлагая его по
первой строке:
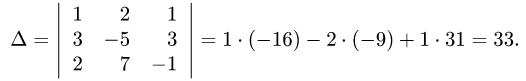
Так как он не равен нулю, то система уравнений имеет единственное
решение.
2.Вычисляем определители
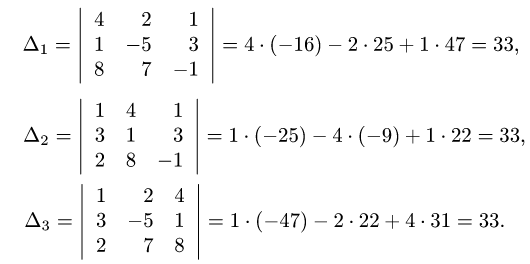
3.По формулам Крамера (1) находим решение системы уравнений
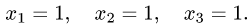
Ответ. 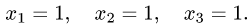
Обратная матрица
Постановка задачи. Задана квадратная матрица третьего
порядка

Установить существование и найти обратную матрицу 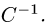
План решения. Матрица 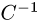 называется обратной квадратной
называется обратной квадратной
матрице С, если
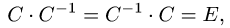
где Е — единичная матрица.
Если 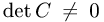 (матрица С — невырожденная), то матрица С
(матрица С — невырожденная), то матрица С
имеет обратную, если det С = 0, то матрица С не имеет обратной.
1.Вычисляем определитель матрицы det С. Если 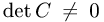 , то
, то
матрица С имеет обратную.
2.Составляем матрицу из алгебраических дополнений
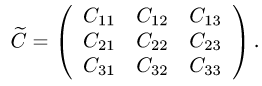
3.Транспонируем матрицу 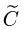
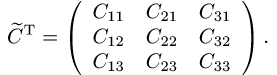
4.Разделив матрицу 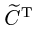 на определитель, получаем искомую обратную матрицу
на определитель, получаем искомую обратную матрицу
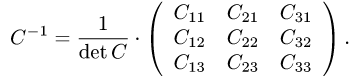
5.Проверяем, что 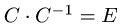 и записываем ответ.
и записываем ответ.
Пример. Задана квадратная матрица третьего порядка
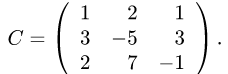
Установить существование и найти обратную матрицу 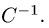
Решение.
1.Вычисляем определитель матрицы detC:
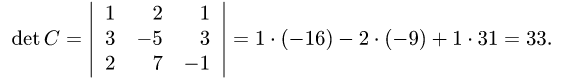
Так как 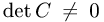 , то матрица С имеет обратную.
, то матрица С имеет обратную.
2.Составляем матрицу из алгебраических дополнений
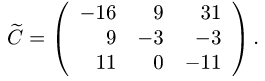
3.Транспонируем матрицу 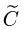
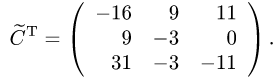
4.Разделив матрицу 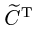 на определитель, получаем искомую обратную матрицу
на определитель, получаем искомую обратную матрицу
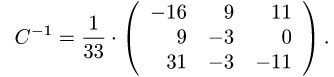
5.Проверяем
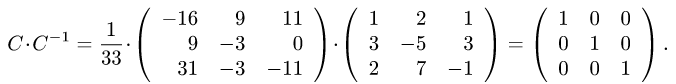
Ответ. Матрица, обратная матрице С, есть
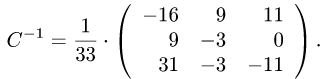
Понятие линейного пространства
Постановка задачи. Образует ли линейное пространство заданное множество X, в котором определены «сумма» а  b любых
b любых
двух элементов а и b и «произведение»  любого элемента а на
любого элемента а на
любое число 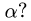
План решения. Исходя из определения линейного пространства,
проверяем следующие условия.
1.Являются ли введенные операции сложения и умножения на
число замкнутыми в X, т.е. верно ли, что 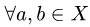 и
и 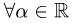
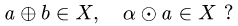
Если нет, то множество X не является линейным пространством, если
да, то продолжаем проверку.
2.Находим нулевой элемент 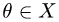 такой, что
такой, что 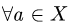
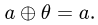
Если такого элемента не существует, то множество X не является
линейным пространством, если существует, то продолжаем проверку.
3.Для каждого элемента 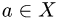 определяем противоположный элемент
определяем противоположный элемент 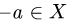 такой, что
такой, что
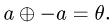
Если такого элемента не существует, то множество X не является
линейным пространством, если существует, то продолжаем проверку.
4.Проверяем выполнение остальных аксиом линейного пространства, т.е. 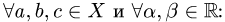
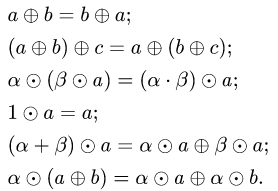
Если хотя бы одна из аксиом нарушается, то множество X не
является линейным пространством. Если выполнены все аксиомы, то
множество X — линейное пространство.
Пример. Образует ли линейное пространство множество положительных чисел 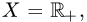 в котором операции «сложения» и «умножения на число» определены следующим образом:
в котором операции «сложения» и «умножения на число» определены следующим образом: 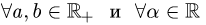
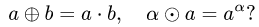
Решение.
1.Введенные таким образом операции являются замкнутыми в
данном множестве, так как если 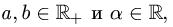 то
то
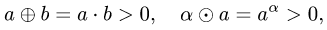
т.е. 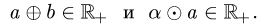
2.В качестве нулевого элемента нужно взять единицу 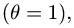 так
так
как
а • 1 = а,
иными словами,
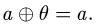
3.В качестве элемента —а, противоположного элементу а, нужно
взять 1/а, так как
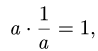
иными словами,
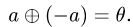
4.Проверяем выполнение остальных аксиом линейного пространства, т.е. 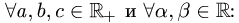
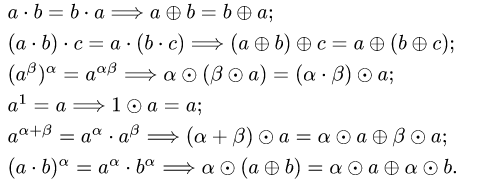
Все аксиомы выполнены.
Системы линейных уравнений
Задача 1. Однородные системы уравнений
Постановка задачи. Найти размерность d пространства решений, его базис (фундаментальную систему решении) и общее решение однородной системы линейных уравнений
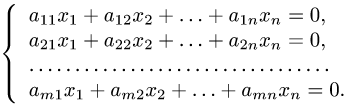
План решения.
1.Записываем матрицу системы:

и с помощью элементарных преобразований строк преобразуем матрицу А так, чтобы в максимальном числе столбцов оказалось по одной единице (в разных строках у разных столбцов), а остальные элементы столбцов были нулями. Очевидно, что такие столбцы линейно независимы. Они называются базисными.
Полученную матрицу будем называть редуцированной и обозначать 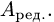 Отметим, что редуцированная матрица эквивалентна исходной
Отметим, что редуцированная матрица эквивалентна исходной 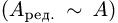 и система уравнений с матрицей
и система уравнений с матрицей 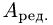 эквивалентна исходной системе уравнений.
эквивалентна исходной системе уравнений.
2. Так как 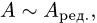 то вычисляем ранг А как количество базис-
то вычисляем ранг А как количество базис-
базисных столбцов матрицы 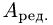 :
:
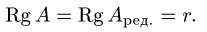
Следовательно, размерность пространства решений есть d = n — r.
Если n = r, то однородная система имеет единственное (нулевое)
решение, если n > r, то фундаментальная система состоит из n — r
линейно независимых решений.
3.Неизвестные, соответствующие базисным столбцам, называются базисными, остальные — свободными (или параметрическими).
Запишем систему уравнений с матрицей 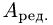 и перенесем n — r
и перенесем n — r
свободных неизвестных в правые части уравнений системы. Придавая свободным неизвестным n — r наборов значений (по одной единице, остальные — нули), для каждого такого набора решаем систему уравнений и находим соответствующие значения базисных
неизвестных. Убедимся, что полученные решения  линейно независимы, составив матрицу из столбцов
линейно независимы, составив матрицу из столбцов  и вычислив ее ранг.
и вычислив ее ранг.
Записываем фундаментальную систему решений  и общее решение однородной системы линейных уравнений
и общее решение однородной системы линейных уравнений
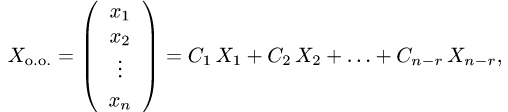
где  — фундаментальная система решений однородной системы линейных уравнений и
— фундаментальная система решений однородной системы линейных уравнений и  — произвольные постоянные.
— произвольные постоянные.
Пример 1. Найти размерность d пространства решений, его базис
(фундаментальную систему решений) и общее решение однородной
системы линейных уравнений
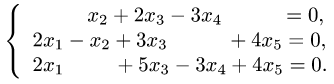
Решение.
1.Записываем матрицу системы и с помощью элементарных преобразований строк преобразуем ее к редуцированному виду:
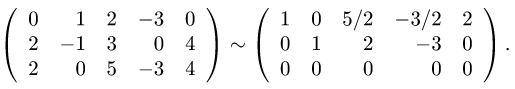
Очевидно, что первый и второй столбцы матрицы 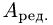 (и исходной
(и исходной
матрицы А) линейно независимы, а остальные столбцы являются их
линейными комбинациями. Поэтому первый и второй столбцы —
базисные.
2.Так как количество линейно независимых столбцов матрицы
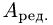 равно двум, то
равно двум, то
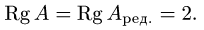
Следовательно, размерность пространства решений
d=n-r=5-2=3
и фундаментальная система решений состоит из трех линейно
независимых решений.
3. Неизвестные 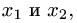 соответствующие базисным столбцам,
соответствующие базисным столбцам,
являются базисными, неизвестные 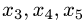 — свободными.
— свободными.
Запишем систему уравнений с матрицей 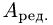 (эта система
(эта система
эквивалентна исходной) и перенесем свободные неизвестные в правые части уравнений системы:
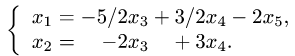
Для первого набора свободных неизвестных 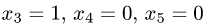
получаем 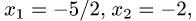 т.е. первое решение имеет вид системы
т.е. первое решение имеет вид системы
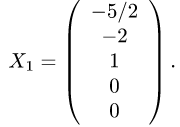
Для второго набора свободных неизвестных 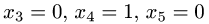
получаем 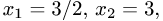 т.е. второе решение имеет вид системы
т.е. второе решение имеет вид системы
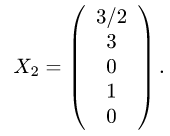
Для третьего набора свободных неизвестных 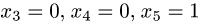
получаем 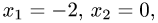 т.е. третье решение системы имеет вид
т.е. третье решение системы имеет вид
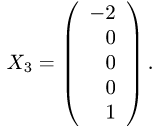
Сделаем проверку, подставив эти решения в исходную систему
уравнений, а также убедимся, что решения линейно независимы (ранг матрицы, составленной из столбцов 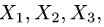 равен 3).
равен 3).
Следовательно, решения 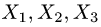 образуют базис в пространстве решений (фундаментальную систему решений).
образуют базис в пространстве решений (фундаментальную систему решений).
Ответ. Размерность пространства решений есть d = 3. Фундаментальная система решений есть
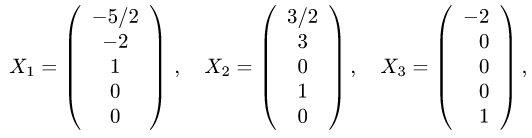
и общее решение однородной системы имеет вид
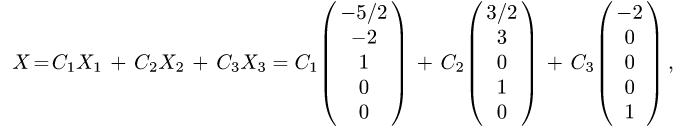
где 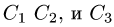 — произвольные постоянные.
— произвольные постоянные.
Задача 2. Неоднородные системы уравнений
Постановка задачи. Найти общее решение неоднородной системы линейных уравнений
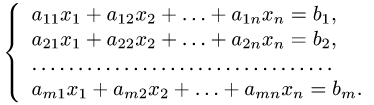
План решения.
1.Записываем расширенную матрицу системы
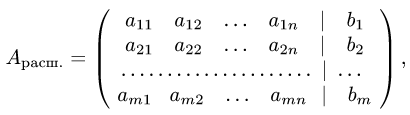
и с помощью элементарных преобразований строк преобразуем матрицу 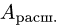 к редуцированному виду.
к редуцированному виду.
2.Вычисляем ранги основной матрицы системы А и расширенной
матрицы 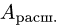 . Если
. Если 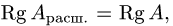 то система совместна, если
то система совместна, если
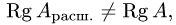 то система несовместна (решений не имеет).
то система несовместна (решений не имеет).
3.Пусть 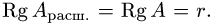 Тогда общее решение неоднородной системы линейных уравнений определяется формулой
Тогда общее решение неоднородной системы линейных уравнений определяется формулой
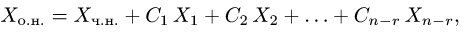
где 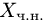 — какое-либо частное решение неоднородной системы,
— какое-либо частное решение неоднородной системы,
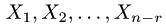 — фундаментальная система решений соответствующей однородной системы и
— фундаментальная система решений соответствующей однородной системы и  — произвольные постоянные.
— произвольные постоянные.
Чтобы найти фундаментальную систему решений однородной сис-
системы уравнений 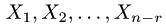 , повторим операции, изложенные в задаче 1.
, повторим операции, изложенные в задаче 1.
4.Столбец свободных членов В расширенной матрицы есть линейная комбинация базисных столбцов матрицы А. Добавляя к этому выражению остальные столбцы с нулевыми коэффициентами, получаем разложение столбца свободных членов по всем столбцам матрицы А. Коэффициенты этого разложения образуют частное решение неоднородной системы 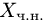 .
.
5.Записываем общее решение неоднородной системы линейных
уравнений:
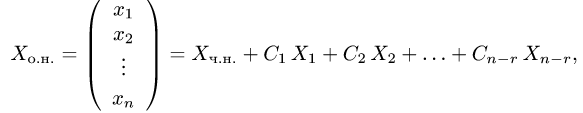
где 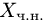 — какое-нибудь частное решение неоднородной системы,
— какое-нибудь частное решение неоднородной системы,
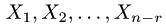 — фундаментальная система решений соответствующей однородной системы уравнений и
— фундаментальная система решений соответствующей однородной системы уравнений и  — произвольные постоянные.
— произвольные постоянные.
Пример 2. Найти общее решение неоднородной системы линейных уравнений
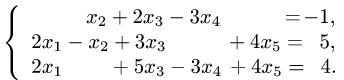
Решение.
1.Записываем расширенную матрицу системы и с помощью элементарных преобразований строк преобразуем матрицу 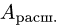 к
к
редуцированному виду:
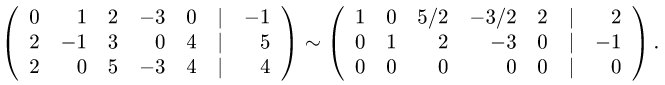
2.Так как 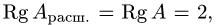 то система совместна. Так как
то система совместна. Так как
n — r = 5 — 2 = 3, то общее решение неоднородной системы линейных
уравнений определяется формулой
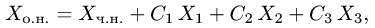
где 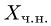 — какое-нибудь частное решение неоднородной системы,
— какое-нибудь частное решение неоднородной системы,
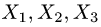 — фундаментальная система решений соответствующей однородной системы и
— фундаментальная система решений соответствующей однородной системы и 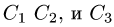 — произвольные постоянные.
— произвольные постоянные.
3.Запишем соответствующую однородную систему уравнений
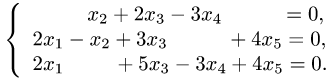
Она совпадает с системой, приведенной в примере 1. (Если однородная система уравнений не совпадает с системой, приведенной в примере 1, то для нахождения фундаментальной системы решений повторим операции, использованные при решении примера 1.)
При решении примера 1 была найдена фундаментальная система
решений однородной системы уравнений:
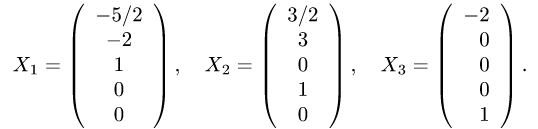
4.Найдем какое-нибудь частное решение неоднородной системы.
Столбец свободных членов В расширенной матрицы есть линейная
комбинация базисных столбцов матрицы А, т.е. столбцов 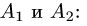
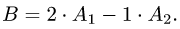
Добавляя к этому выражению остальные столбцы с нулевыми коэффициентами, получим
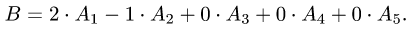
Коэффициенты в этом разложении образуют частное решение неоднородной системы
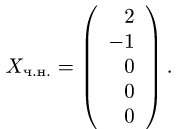
Сделаем проверку, подставив 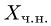 в исходную систему уравнений.
в исходную систему уравнений.
Ответ. Общее решение системы имеет вид
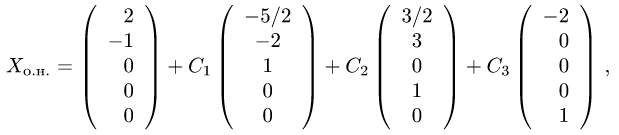
где 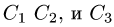 — произвольные постоянные.
— произвольные постоянные.
Линейные операторы
Постановка задачи. Пусть в некотором базисе линейного пространства 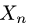 задан произвольный вектор
задан произвольный вектор 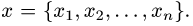 Является ли линейным оператор
Является ли линейным оператор 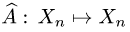 такой, что
такой, что
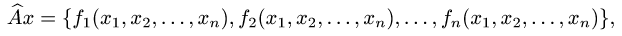
где 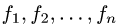 — некоторые функции п переменных?
— некоторые функции п переменных?
План решения. Если 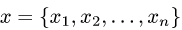 и
и 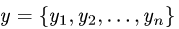 —
—
произвольные векторы пространства 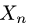 , то
, то 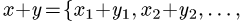
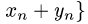 и
и 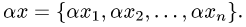
Проверяем условия линейности оператора:
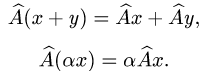
Если условия линейности выполнены, т.е.
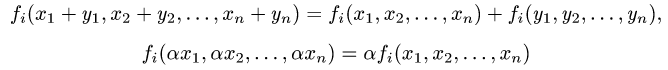
при i = 1, 2,…, n, то оператор 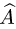 линеен, в противном случае
линеен, в противном случае
оператор 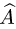 нелинеен.
нелинеен.
Пример. Пусть в некотором базисе линейного пространства 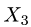
задан произвольный вектор 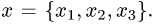 Является ли линейным оператор
Является ли линейным оператор 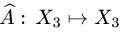 такой, что
такой, что
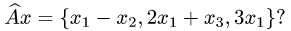
Решение. Пусть 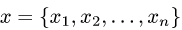 и
и 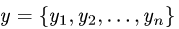 — произвольные векторы пространства
— произвольные векторы пространства 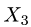 . Тогда
. Тогда 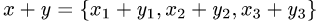 и
и
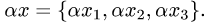
Проверяем условия линейности оператора:
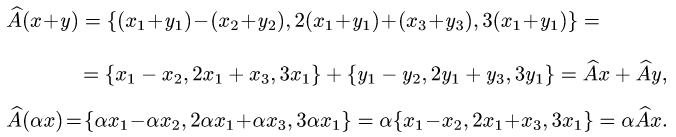
Условия линейности выполнены. Следовательно, оператор 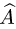 линеен.
линеен.
Ответ. Оператор 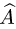 линеен.
линеен.
Матрица, образ, ядро, ранг и дефект оператора
Постановка задачи. Задан оператор 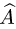 , осуществляющий некоторое преобразование пространства геометрических векторов
, осуществляющий некоторое преобразование пространства геометрических векторов 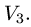
Доказать линейность, найти матрицу (в базисе 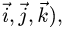 образ, ядро,
образ, ядро,
ранг и дефект оператора 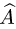 .
.
План решения.
1.По определению доказываем линейность оператора 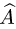 , используя свойства операций над геометрическими векторами в координатной форме, т.е. проверяем, что
, используя свойства операций над геометрическими векторами в координатной форме, т.е. проверяем, что 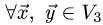 и
и 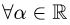
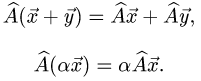
2.Строим по определению матрицу оператора 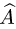 . Для этого находим образы базисных векторов
. Для этого находим образы базисных векторов 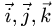 и записываем их координаты
и записываем их координаты
в базисе 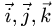 . Столбцы искомой матрицы — это столбцы координат
. Столбцы искомой матрицы — это столбцы координат
образов базисных векторов.
3.Находим образ, ранг, ядро и дефект оператора 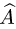 , исходя из их
, исходя из их
определений.
Пример. Доказать линейность, найти матрицу (в базисе 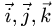 ),
),
образ, ядро, ранг и дефект оператора проецирования пространства
геометрических векторов 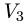 на плоскость XOY.
на плоскость XOY.
Решение.
1.Докажем по определению линейность оператора проецирования. Пусть в базисе 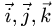 имеем произвольный вектор
имеем произвольный вектор 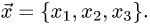
Тогда его образ (проекция) есть 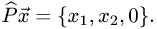
По правилам операций с геометрическими векторами в координатной форме 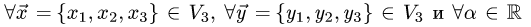 имеем
имеем
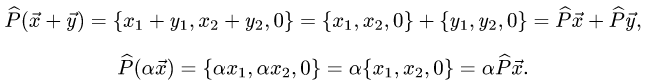
2.Так как по определению матрицы оператора ее столбцы —
это столбцы координат образов базисных векторов, найдем образы
базисных векторов 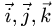 и запишем их координаты в базисе
и запишем их координаты в базисе 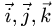 :
:
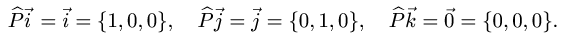
Таким образом, матрица оператора проецирования 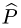 есть
есть
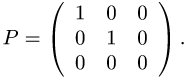
3.Находим образ, ранг, ядро и дефект оператора 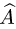 , исходя из
, исходя из
определений.
Образ оператора проецирования 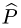 — это множество векторов,
— это множество векторов,
лежащих в плоскости XOY, следовательно, в базисе 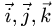
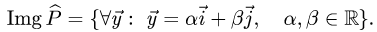
Отсюда 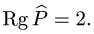
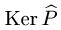 — это множество векторов, коллинеарных оси OZ, следовательно, в базисе
— это множество векторов, коллинеарных оси OZ, следовательно, в базисе 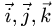
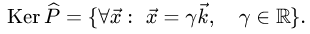
Отсюда 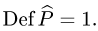
Заметим, что 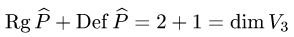
Ответ. Оператор 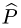 линеен. Его матрица в базисе
линеен. Его матрица в базисе 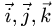 есть
есть
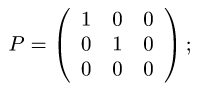
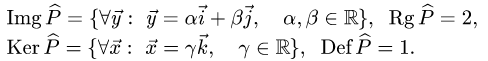
Действия с операторами и их матрицами
Постановка задачи. В некотором базисе трехмерного линейного пространства 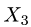 заданы отображения
заданы отображения
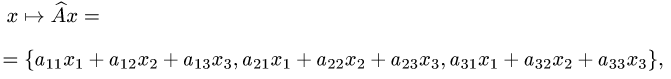
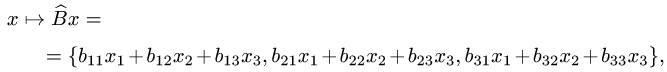
где 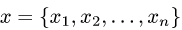 — произвольный вектор пространства
— произвольный вектор пространства 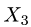 .
.
Найти координаты вектора 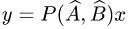 (в том же базисе), где
(в том же базисе), где
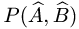 — многочлен относительно операторов
— многочлен относительно операторов 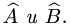
План решения. Так как при сложении операторов их матрицы
складываются, при умножении на число — умножаются на это число,
а матрица композиции операторов равна произведению их матриц,
то нужно найти матрицу Р(А, В), где А и В — матрицы операторов
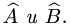 Затем столбец координат вектора
Затем столбец координат вектора 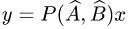 находим по формуле Р(А, В) • X, где X — столбец координат вектора х.
находим по формуле Р(А, В) • X, где X — столбец координат вектора х.
1.Построим матрицы операторов 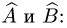
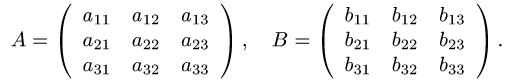
2.По правилам сложения матриц, умножения матрицы на число и
умножения матриц находим матрицу Р(А,В):
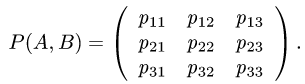
3.Находим столбец координат образа вектора х:
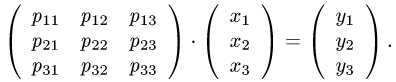
Записываем ответ в виде 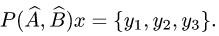
Пример. В некотором базисе трехмерного линейного пространства 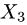 заданы отображения
заданы отображения
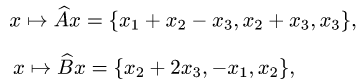
где 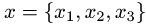 — произвольный вектор пространства
— произвольный вектор пространства 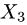 . Найти координаты вектора
. Найти координаты вектора 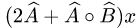 в том же базисе.
в том же базисе.
Решение.
1.Построим матрицы операторов 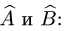
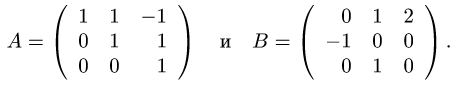
2.По правилам сложения матриц, умножения матрицы на число и
умножения матриц вычисляем матрицу 2А + А • В:
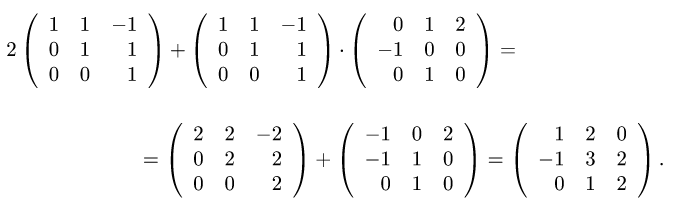
3.Находим столбец координат образа вектора х:
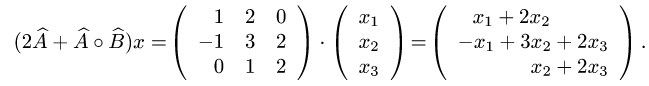
Ответ. 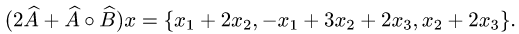
Преобразование координат вектора
Постановка задачи. Вектор х в базисе 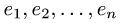 имеет координаты
имеет координаты 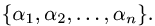 Найти координаты вектора х в базисе
Найти координаты вектора х в базисе
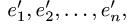 где
где
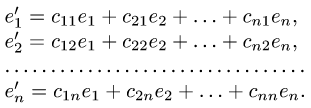
План решения. Координаты вектора при переходе от базиса
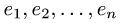 к базису
к базису 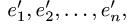 преобразуются по формуле
преобразуются по формуле

где 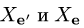 — столбцы координат вектора х в базисах
— столбцы координат вектора х в базисах 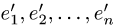 и
и 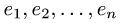 , G — матрица перехода от базиса
, G — матрица перехода от базиса 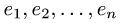 к базису
к базису 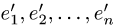 .
.
1.Находим матрицу перехода С. Так как столбцы матрицы перехода от базиса 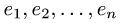 к базису
к базису 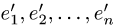 — это столбцы
— это столбцы
координат векторов 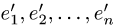 в базисе
в базисе 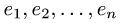 , то матрица перехода имеет вид
, то матрица перехода имеет вид

2.Находим обратную матрицу 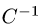 и проверяем, что
и проверяем, что 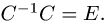
3.По формуле (1) находим столбец координат вектора х в базисе
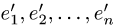 :
:
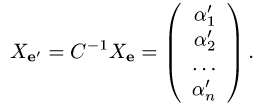
Записываем ответ в виде 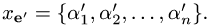
Пример. Вектор х в базисе 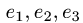 имеет координаты {1,2,3}.
имеет координаты {1,2,3}.
Найти координаты вектора х в базисе 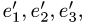 где
где
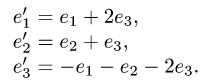
Решение.
1.Находим матрицу перехода
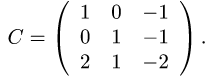
2.Находим обратную матрицу 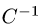 методом Гаусса:
методом Гаусса:
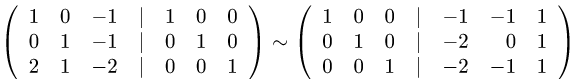
Таким образом,
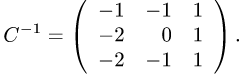
Проверяем, что 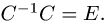
3.По формуле (1) находим столбец координат вектора х в базисе
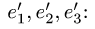
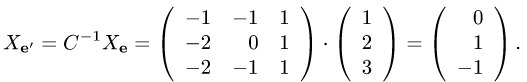
Ответ. 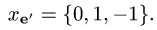
Преобразование матрицы оператора
Постановка задачи. Найти матрицу некоторого оператора 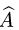 в базисе
в базисе 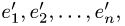 где
где
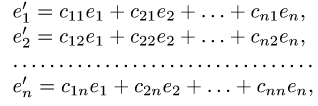
если в базисе 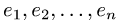 его матрица имеет вид
его матрица имеет вид

План решения. При переходе от базиса 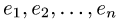 к базису
к базису
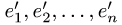 матрица оператора преобразуется по формуле
матрица оператора преобразуется по формуле

где С — матрица перехода от базиса 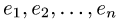 к базису
к базису 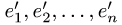
1.Находим матрицу перехода С. Так как столбцы матрицы пе-
перехода от базиса 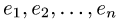 к базису
к базису 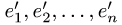 — это столбцы координат векторов
— это столбцы координат векторов 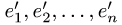 в базисе
в базисе 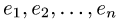 , то
, то

2.Находим обратную матрицу 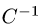 и проверяем, что
и проверяем, что 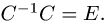
3.Находим матрицу оператора 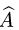 в базисе
в базисе 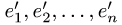 по формуле (1)
по формуле (1)
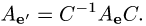
Пример. Найти матрицу оператора 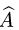 в базисе
в базисе 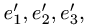 где
где
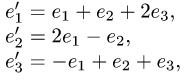
если в базисе 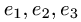 его матрица имеет вид
его матрица имеет вид
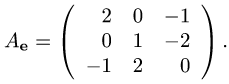
Решение.
1.Находим матрицу перехода
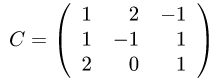
2.Находим обратную матрицу 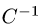 методом Гаусса:
методом Гаусса:
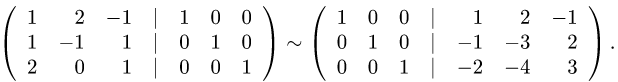
Таким образом,
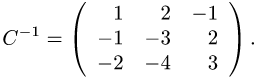
Убеждаемся, что 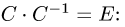
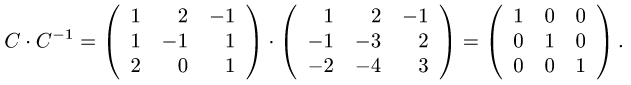
3.Находим матрицу оператора 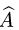 в базисе
в базисе 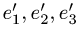 по формуле (1)
по формуле (1)
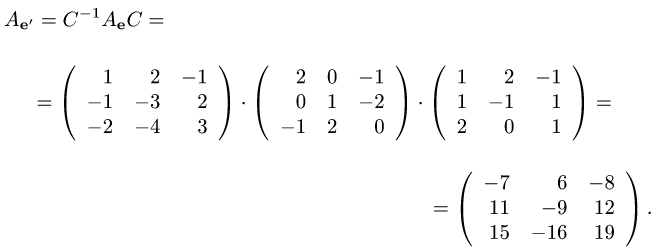
Ответ. 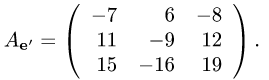
Собственные значения и собственные векторы оператора
Постановка задачи. Найти собственные значения и собственные векторы оператора 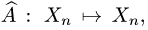 заданного в некотором
заданного в некотором
базисе матрицей

План решения. Собственные значения оператора 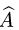 являются
являются
корнями его характеристического уравнения 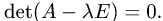
1.Составляем характеристическое уравнение и находим все его
вещественные корни (среди них могут быть и кратные).
2.Для каждого собственного значения 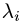 найдем собственные векторы. Для этого записываем однородную систему уравнений
найдем собственные векторы. Для этого записываем однородную систему уравнений
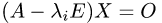
и находим фундаментальную систему решений 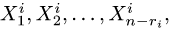 где
где
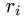 — ранг матрицы системы
— ранг матрицы системы 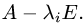 (Заметим, что
(Заметим, что 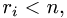 так как
так как 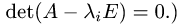
3.Столбцы  являются столбцами координат искомых собственных векторов
являются столбцами координат искомых собственных векторов 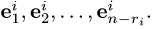 Окончательно для
Окончательно для 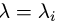 записываем ответ в виде
записываем ответ в виде
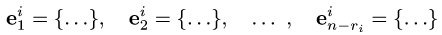
Замечание. Множество собственных векторов, соответствующих собственному значению 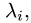 можно записать в виде
можно записать в виде
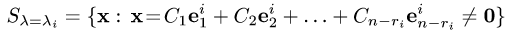
Пример. Найти собственные значения и собственные векторы оператора 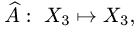 заданного в некотором базисе матрицей
заданного в некотором базисе матрицей
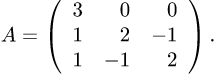
Решение.
1.Составляем характеристическое уравнение:
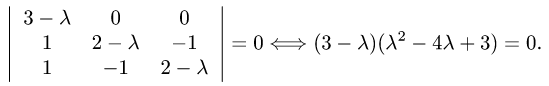
Поэтому 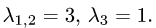
2.Для собственного значения 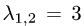 найдем собственные векторы. Запишем однородную систему уравнений (А — 3 • Е)Х = О:
найдем собственные векторы. Запишем однородную систему уравнений (А — 3 • Е)Х = О:
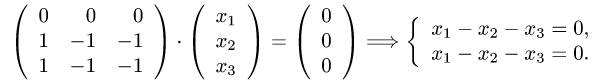
Очевидно, ранг матрицы этой системы равен 1 (n — r = 2 — размерность пространства решений), следовательно, система нетривиально совместна и ее фундаментальная система решений имеет вид
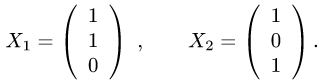
Итак, двукратному собственному значению 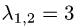 соответствуют
соответствуют
два линейно независимых собственных вектора 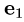 = {1,1,0} и
= {1,1,0} и 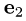 =
=
= {1,0,1}. Множество всех собственных векторов 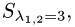
соответствующих собственному значению 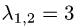 , имеет вид
, имеет вид
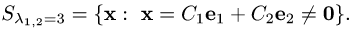
Аналогично находим собственный вектор, соответствующий
собственному значению 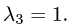 Получим
Получим 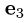 = {0,1,1}. Поэтому множество всех собственных векторов
= {0,1,1}. Поэтому множество всех собственных векторов 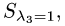 соответствующих
соответствующих
собственному значению 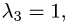 имеет вид
имеет вид
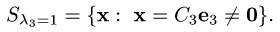
Ответ.
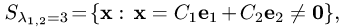 где
где 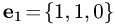 и
и 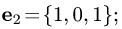
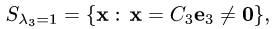 где
где 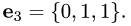
Дополнительные лекции:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат

